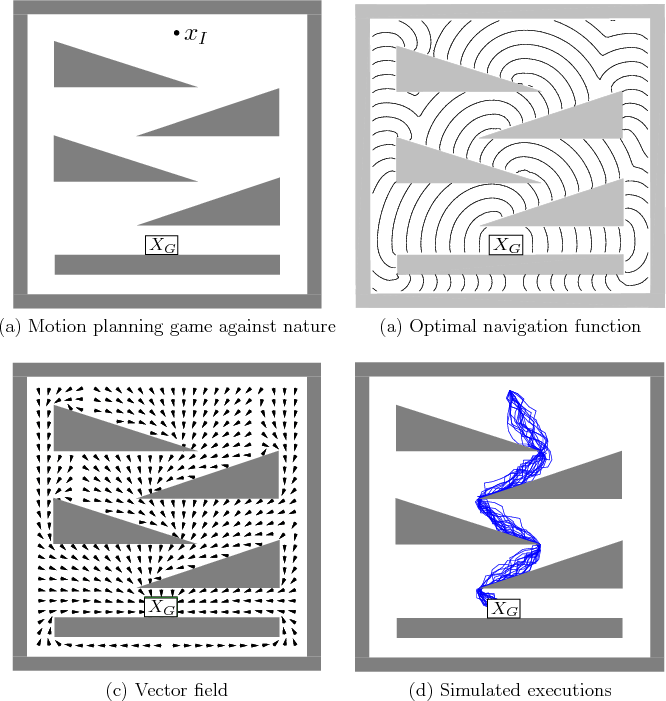
Figure 10.20:
(a) A 2D planning problem is shown in which
nature is probabilistic (uniform density over an interval of angles)
and can interfere with the direction of motion. Contact with
obstacles is actually allowed in this problem. (b) Level sets of the
computed, optimal cost-to-go (navigation) function. (c) The vector
field derived from the navigation function. (d) Several dozen execution
trials are superimposed [605].
 |
Recall from Section 8.5.2 that value iteration with
interpolation can be applied to motion planning problems that are
approximated in discrete time. Nature can even be introduced into the
discrete-time approximation. For example, (8.62) can be
replaced by
 |
(10.123) |
in which  is chosen from a bounded set,
is chosen from a bounded set,
 . Using
(10.124), value iterations can be performed as
described so far. An example of a 2D motion planning problem under
this model using probabilistic uncertainty is shown in Figure
10.20. It is interesting that when the plan is executed from
a fixed initial state, a different trajectory is obtained each time.
The average cost over multiple executions, however, is close to the
expected optimum.
. Using
(10.124), value iterations can be performed as
described so far. An example of a 2D motion planning problem under
this model using probabilistic uncertainty is shown in Figure
10.20. It is interesting that when the plan is executed from
a fixed initial state, a different trajectory is obtained each time.
The average cost over multiple executions, however, is close to the
expected optimum.
Figure 10.21:
Level sets of the optimal navigation
function and resulting vector field are shown for a stochastic, hybrid
motion planning problem. There are two modes, which correspond to
whether a door is closed. The goal is to reach the rectangle at the
bottom left [613]
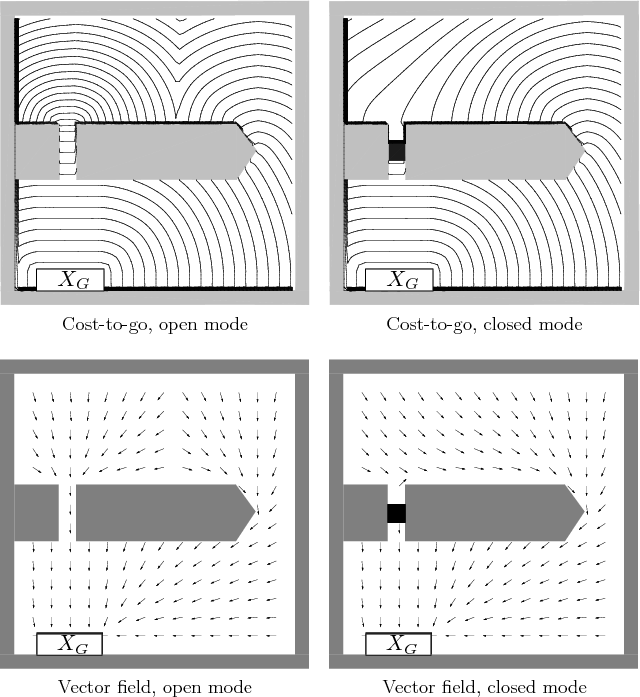 |
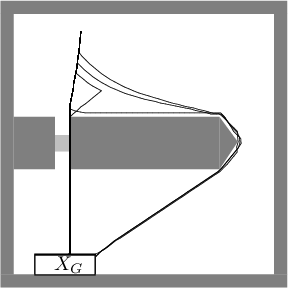
Figure 10.22:
Several executions from the same initial
state are shown. A different trajectory results each time because of
the different times when the door is open or closed.
 |
Interesting hybrid system examples can be made in which nature is only
allowed to interfere with the mode. Recall Formulation 7.3
from Section 7.3. Nature can be added to yield the
following formulation.
Value iteration proceeds in the same way for such hybrid problems.
Interpolation only needs to be performed over the configuration space.
Along the mode ``axis'' no interpolation is needed because the mode
set is already finite. The resulting computation time grows linearly
in the number of modes. A 2D motion planning example for a point
robot, taken from [613], is shown in Figures 10.21
and 10.22. In this case, the environment contains a door
that is modeled as a stationary Markov process. The configuration
space is sampled using a
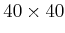 grid. There are two modes:
door open or door closed. Thus, the configuration space has two
layers, one for each mode. The robot wishes to minimize the expected
time to reach the goal. The navigation function for each layer cannot
be computed independently because each takes into account the
transition probabilities for the mode. For example, if the door is
almost always open, then its plan would be different from one in which
the door is almost always closed. If the door is almost always open,
then the robot should go toward the door, even if it is currently
closed, because it is highly likely that it will open soon. Numerous
variations can be made on this example. More modes could be added,
and other interpretations are possible, such as hazardous regions and
shelters (the mode might be imagined as rain occurring and the robot
must run for shelter) or requests to deliver objects
[613,870,871].
grid. There are two modes:
door open or door closed. Thus, the configuration space has two
layers, one for each mode. The robot wishes to minimize the expected
time to reach the goal. The navigation function for each layer cannot
be computed independently because each takes into account the
transition probabilities for the mode. For example, if the door is
almost always open, then its plan would be different from one in which
the door is almost always closed. If the door is almost always open,
then the robot should go toward the door, even if it is currently
closed, because it is highly likely that it will open soon. Numerous
variations can be made on this example. More modes could be added,
and other interpretations are possible, such as hazardous regions and
shelters (the mode might be imagined as rain occurring and the robot
must run for shelter) or requests to deliver objects
[613,870,871].
Steven M LaValle
2020-08-14



