Now consider the probabilistic case. A value iteration method can be
obtained by once again shadowing the presentation in Section
2.3.1. For 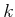 from
from 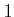 to
to 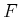 , let
, let 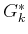 denote the
expected cost from stage
denote the
expected cost from stage 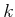 to
to 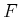 under the execution of the optimal
plan (compare to (2.5)):
under the execution of the optimal
plan (compare to (2.5)):
![$\displaystyle G^*_k(x_k) = \min_{u_k,\ldots,u_K} \left\{ E_{\theta_k,\ldots,\theta_K} \left[ \sum_{i=k}^{K} l(x_i,u_i,\theta_i) + l_F(x_F) \right] \right\} .$](img4059.gif) |
(10.40) |
The optimal cost-to-go for the boundary condition of 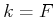 again
reduces to (10.34).
again
reduces to (10.34).
Once again, the algorithm makes 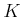 passes over
passes over  , each time
computing
, each time
computing 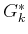 from
from 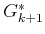 , as
, as 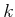 ranges from
ranges from  down
to
down
to 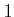 . As before,
. As before, 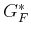 is copied from
is copied from 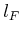 . In the second
iteration,
. In the second
iteration, 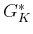 is computed for each
is computed for each 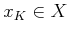 as (compare to
(2.7))
as (compare to
(2.7))
![$\displaystyle G^*_K(x_K) = \min_{u_K} \Big\{ E_{\theta_K} \Big[ l(x_K,u_K,\theta_K) + l_F(x_F) \Big] \Big\},$](img4060.gif) |
(10.41) |
in which
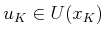 and the expectation occurs over
and the expectation occurs over 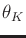 .
Substitutions are made into (10.41) to obtain (compare to
(2.8))
.
Substitutions are made into (10.41) to obtain (compare to
(2.8))
![$\displaystyle G^*_K(x_K) = \min_{u_K} \Big\{ E_{\theta_K} \Big[ l(x_K,u_K,\theta_K) + G^*_F(f(x_K,u_K,\theta_K)) \Big] \Big\} .$](img4062.gif) |
(10.42) |
The general iteration is
![\begin{displaymath}\begin{split}G^*_k(x_k) = & \min_{u_k} \Bigg\{ E_{\theta_k} \...
...eta_i) + l_F(\xKp1) \Bigg] \Bigg\} \Bigg] \Bigg\} , \end{split}\end{displaymath}](img4063.gif) |
(10.43) |
which is obtained once again by pulling the first cost term out of the
sum and by separating the minimization over 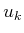 from the rest. The
second
from the rest. The
second 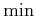 and expectation do not affect the
and expectation do not affect the
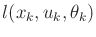 term, which is pulled outside to obtain (compare to
(2.10))
term, which is pulled outside to obtain (compare to
(2.10))
![\begin{displaymath}\begin{split}G^*_k({x_k}) = & \min_{{u_k}} \Bigg\{ E_{{\theta...
...theta_i) + l(\xKp1) \Bigg] \Bigg\} \Bigg] \Bigg\} . \end{split}\end{displaymath}](img4064.gif) |
(10.44) |
The inner  and expectation define
and expectation define 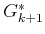 , yielding the
recurrence (compare to (2.11) and (10.39))
, yielding the
recurrence (compare to (2.11) and (10.39))
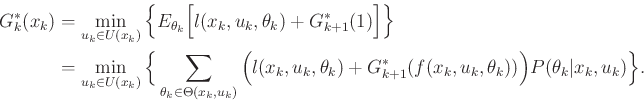 |
(10.45) |
If the cost term does not depend on
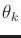 , it can be written as
, it can be written as
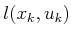 , and (10.45) simplifies to
, and (10.45) simplifies to
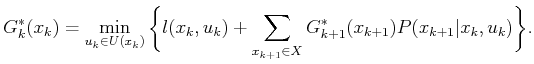 |
(10.46) |
The dependency of state transitions on 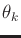 is implicit through
the expression of
is implicit through
the expression of
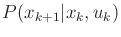 , for which the definition uses
, for which the definition uses
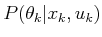 and the state transition equation
and the state transition equation  . The
form given in (10.46) may be more convenient than
(10.45) in implementations.
. The
form given in (10.46) may be more convenient than
(10.45) in implementations.
Steven M LaValle
2020-08-14

![]() from
from ![]() to
to ![]() , let
, let ![]() denote the
expected cost from stage
denote the
expected cost from stage ![]() to
to ![]() under the execution of the optimal
plan (compare to (2.5)):
under the execution of the optimal
plan (compare to (2.5)):
![]() passes over
passes over ![]() , each time
computing
, each time
computing ![]() from
from ![]() , as
, as ![]() ranges from
ranges from ![]() down
to
down
to ![]() . As before,
. As before, ![]() is copied from
is copied from ![]() . In the second
iteration,
. In the second
iteration, ![]() is computed for each
is computed for each ![]() as (compare to
(2.7))
as (compare to
(2.7))
![]() , it can be written as
, it can be written as
![]() , and (10.45) simplifies to
, and (10.45) simplifies to