The closure constraints introduced in Section 4.4 can be
summarized as follows. There is a set, 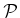 , of polynomials
, of polynomials
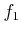 ,
,  ,
, 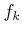 that belong to
that belong to
![$ {\mathbb{Q}}[q_1,\ldots,q_n]$](img2774.gif) and express
the constraints for particular points on the links of the robot. The
determination of these is detailed in Section 4.4.3. As
mentioned previously, polynomials that force points to lie on a circle
or sphere in the case of rotations may also be included in
and express
the constraints for particular points on the links of the robot. The
determination of these is detailed in Section 4.4.3. As
mentioned previously, polynomials that force points to lie on a circle
or sphere in the case of rotations may also be included in 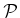 .
.
Let  denote the dimension of
denote the dimension of  . The closure space is
defined as
. The closure space is
defined as
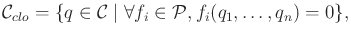 |
(7.21) |
which is an 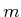 -dimensional subspace of
-dimensional subspace of  that corresponds to all
configurations that satisfy the closure constants. The obstacle set
must also be taken into account. Once again,
that corresponds to all
configurations that satisfy the closure constants. The obstacle set
must also be taken into account. Once again,
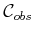 and
and
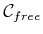 are
defined using (4.34). The feasible
space is defined as
are
defined using (4.34). The feasible
space is defined as
 , which are the configurations that satisfy
closure constraints and avoid collisions.
, which are the configurations that satisfy
closure constraints and avoid collisions.
The motion planning problem is to find a path
![$ \tau: [0,1] \rightarrow
{{\cal C}_{fea}}$](img2777.gif) such that
such that
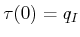 and
and
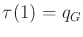 . The new
challenge is that there is no explicit parameterization of
. The new
challenge is that there is no explicit parameterization of
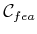 ,
which is further complicated by the fact that
,
which is further complicated by the fact that 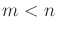 (recall that
(recall that 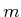 is the dimension of
is the dimension of
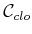 ).
).
Steven M LaValle
2020-08-14

![]() denote the dimension of
denote the dimension of ![]() . The closure space is
defined as
. The closure space is
defined as
![]() such that
such that
![]() and
and
![]() . The new
challenge is that there is no explicit parameterization of
. The new
challenge is that there is no explicit parameterization of
![]() ,
which is further complicated by the fact that
,
which is further complicated by the fact that ![]() (recall that
(recall that ![]() is the dimension of
is the dimension of
![]() ).
).