4.4.3 Defining the Variety for General Linkages

We now describe a general methodology for defining the variety. Keeping the previous examples in mind will help in understanding the formulation. In the general case, each constraint can be thought of as a statement of the form:

The $i$

th

coordinate of a point $p \in {\cal A}_j$ needs to be held at the value $x$ in the body frame of ${\cal A}_k$.

For the variety in Figure 4.23b, the first coordinate of a point $p \in {\cal A}_2$ was held at the value 0 in ${\cal W}$ in the body frame of ${\cal A}_1$. The general form must also allow a point to be fixed with respect to the body frames of links other than ${\cal A}_1$; this did not occur for the example in Section 4.4.2

Suppose that $n$ links, ${\cal A}_1$,$\ldots$, ${\cal A}_n$, move in ${\cal W}= {\mathbb{R}}^2$ or ${\cal W}= {\mathbb{R}}^3$. One link, ${\cal A}_1$ for convenience, is designated as the root as defined in Section 3.4. Some links are attached in pairs to form joints. A linkage graph, ${\cal G}(V,E)$, is constructed from the links and joints. Each vertex of ${\cal G}$ represents a link in $L$. Each edge in ${\cal G}$ represents a joint. This definition may seem somewhat backward, especially in the plane because links often look like edges and joints look like vertices. This alternative assignment is also possible, but it is not easy to generalize to the case of a single link that has more than two joints. If more than two links are attached at the same point, each generates an edge of ${\cal G}$.

Figure 4.27: A complicated linkage that has $29$ links, several loops, links with more than two bodies, and bodies with more than two links. Each integer $i$ indicates link ${\cal A}_i$.

Figure 4.28: (a) One way to make the linkage graph that corresponds to the linkage in Figure 4.27. (b) A spanning tree is indicated by showing the removed edges with dashed lines.

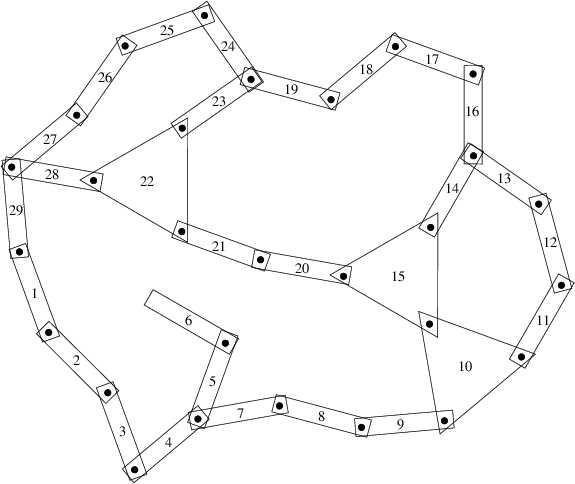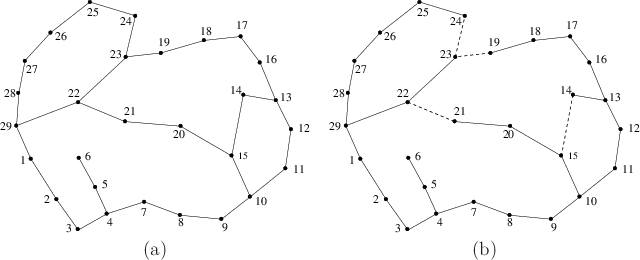The steps to determine the polynomial constraints that express the variety are as follows:

1. Define the linkage graph ${\cal G}$ with one vertex per link and one edge per joint. If a joint connects more than two bodies, then one body must be designated as a junction. See Figures 4.27 and 4.28a. In Figure 4.28, links $4$, $13$, and $23$ are designated as junctions in this way.
2. Designate one link as the root, ${\cal A}_1$. This link may either be fixed in ${\cal W}$, or transformations may be applied. In the latter case, the set of transformations could be $SE(2)$ or $SE(3)$, depending on the dimension of ${\cal W}$. This enables the entire linkage to move independently of its internal motions.
3. Eliminate the loops by constructing a spanning tree $T$ of the linkage graph, ${\cal G}$. This implies that every vertex (or link) is reachable by a path from the root). Any spanning tree may be used. Figure 4.28b shows a resulting spanning tree after deleting the edges shown with dashed lines.
4. Apply the techniques of Section 3.4 to assign body frames and transformations to the resulting tree of links.
5. For each edge of ${\cal G}$ that does not appear in $T$, write a set of constraints between the two corresponding links. In Figure 4.28b, it can be seen that constraints are needed between four pairs of links: $14$-$15$, $21$-$22$, $23$-$24$, and $19$-$23$.

   This is perhaps the trickiest part. For examples like the one shown in Figure 3.27, the constraint may be formulated as in (3.81). This is equivalent to what was done to obtain the example in Figure 4.26, which means that there are actually two constraints, one for each of the $x$ and $y$ coordinates. This will also work for the example shown in Figure 4.27 if all joints are revolute. Suppose instead that two bodies, ${\cal A}_j$ and ${\cal A}_k$, must be rigidly attached. This requires adding one more constraint that prevents mutual rotation. This could be achieved by selecting another point on ${\cal A}_j$ and ensuring that one of its coordinates is in the correct position in the body frame of ${\cal A}_k$. If four equations are added, two from each point, then one of them would be redundant because there are only three degrees of freedom possible for ${\cal A}_j$ relative to ${\cal A}_k$ (which comes from the dimension of $SE(2)$).

   A similar but more complicated situation occurs for ${\cal W}= {\mathbb{R}}^3$. Holding a single point fixed produces three constraints. If a single point is held fixed, then ${\cal A}_j$ may achieve any rotation in $SO(3)$ with respect to ${\cal A}_k$. This implies that ${\cal A}_j$ and ${\cal A}_k$ are attached by a spherical joint. If they are attached by a revolute joint, then two more constraints are needed, which can be chosen from the coordinates of a second point. If ${\cal A}_j$ and ${\cal A}_k$ are rigidly attached, then one constraint from a third point is needed. In total, however, there can be no more than six independent constraints because this is the dimension of $SE(3)$.

6. Convert the trigonometric functions to polynomials. For any 2D transformation, the familiar substitution of complex numbers may be made. If the DH parameterization is used for the 3D case, then each of the $\cos\theta_i$, $\sin\theta_i$ expressions can be parameterized with one complex number, and each of the $\cos\alpha_i$, $\sin\alpha_i$ expressions can be parameterized with another. If the rotation matrix for $SO(3)$ is directly used in the parameterization, then the quaternion parameterization should be used. In all of these cases, polynomial expressions are obtained.
7. List the constraints as polynomial equations of the form $f = 0$. To write the description of the variety, all of the polynomials must be set equal to zero, as was done for the examples in Section 4.4.2.

Is it possible to determine the dimension of the variety from the number of independent constraints? The answer is generally no, which can be easily seen from the chains of links in Section 4.4.2; they produced varieties of various dimensions, depending on the particular equations. Techniques for computing the dimension exist but require much more machinery than is presented here (see the literature overview at the end of the chapter). However, there is a way to provide a simple upper bound on the number of degrees of freedom. Suppose the total degrees of freedom of the linkage in spanning tree form is $m$. Each independent constraint can remove at most one degree of freedom. Thus, if there are $l$ independent constraints, then the variety can have no more than $m - l$ dimensions. One expression of this for a general class of mechanisms is the Kutzbach criterion; the planar version of this is called Grübler's formula [310].

One final concern is the obstacle region, ${\cal C}_{obs}$. Once the variety has been identified, the obstacle region and motion planning definitions in (4.34) and Formulation 4.1 do not need to be changed. The configuration space ${\cal C}$ must be redefined, however, to be the set of configurations that satisfy the closure constraints.