
Next: 7.4.1 Adaptation of Motion Up: 7. Extensions of Basic Previous: Multiple parts
This section continues where Section 4.4 left off. The
subspace of ![]() that results from maintaining kinematic closure was
defined and illustrated through some examples. Planning in this
context requires that paths remain on a lower dimensional variety for
which a parameterization is not available. Many important
applications require motion planning while maintaining these
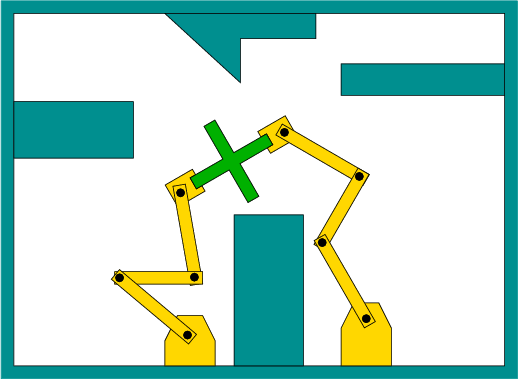
constraints. For example, consider a manipulation problem that
involves multiple manipulators grasping the same object, which forms a
closed loop as shown in Figure 7.19. A loop exists
because both manipulators are attached to the ground, which may itself
be considered as a link. The development of virtual actors for movies
and video games also involves related manipulation problems. Loops
also arise in this context when more than one human limb is touching a
fixed surface (e.g., two feet on the ground). A class of robots
called parallel manipulators are intentionally designed with internal closed loops
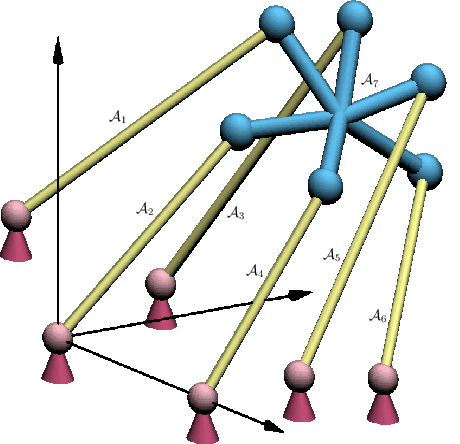
[693]. For example, consider the Stewart-Gough platform
[407,914] illustrated in Figure 7.20. The
lengths of each of the six arms,
that results from maintaining kinematic closure was
defined and illustrated through some examples. Planning in this
context requires that paths remain on a lower dimensional variety for
which a parameterization is not available. Many important
applications require motion planning while maintaining these
constraints. For example, consider a manipulation problem that
involves multiple manipulators grasping the same object, which forms a
closed loop as shown in Figure 7.19. A loop exists
because both manipulators are attached to the ground, which may itself
be considered as a link. The development of virtual actors for movies
and video games also involves related manipulation problems. Loops
also arise in this context when more than one human limb is touching a
fixed surface (e.g., two feet on the ground). A class of robots
called parallel manipulators are intentionally designed with internal closed loops
[693]. For example, consider the Stewart-Gough platform
[407,914] illustrated in Figure 7.20. The
lengths of each of the six arms,
![]() ,
, ![]() ,
,
![]() , can be
independently varied while they remain attached via spherical joints
to the ground and to the platform, which is
, can be
independently varied while they remain attached via spherical joints
to the ground and to the platform, which is
![]() . Each arm
can actually be imagined as two links that are connected by a
prismatic joint. Due to the total of
. Each arm
can actually be imagined as two links that are connected by a
prismatic joint. Due to the total of ![]() degrees of freedom
introduced by the variable lengths, the platform actually achieves the
full
degrees of freedom
introduced by the variable lengths, the platform actually achieves the
full ![]() degrees of freedom (hence, some six-dimensional region in
degrees of freedom (hence, some six-dimensional region in
![]() is obtained for
is obtained for
![]() ). Planning the motion of the
Stewart-Gough platform, or robots that are based on the platform (the
robot shown in Figure 7.27 uses a stack of several of
these mechanisms), requires handling many closure constraints that
must be maintained simultaneously. Another application is
computational biology, in which the C-space of molecules is searched,
many of which are derived from molecules that have closed, flexible
chains of bonds [245].
). Planning the motion of the
Stewart-Gough platform, or robots that are based on the platform (the
robot shown in Figure 7.27 uses a stack of several of
these mechanisms), requires handling many closure constraints that
must be maintained simultaneously. Another application is
computational biology, in which the C-space of molecules is searched,
many of which are derived from molecules that have closed, flexible
chains of bonds [245].
 |
 |