Assume that 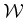 ,
, 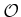 , and
, and 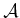 from Formulation 4.1 are
used. For manipulation planning,
from Formulation 4.1 are
used. For manipulation planning, 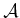 is called the manipulator, and let
is called the manipulator, and let
 refer to the manipulator
configuration space. Let
refer to the manipulator
configuration space. Let  denote a part, which is a
rigid body modeled in terms of geometric primitives, as described in
Section 3.1. It is assumed that
denote a part, which is a
rigid body modeled in terms of geometric primitives, as described in
Section 3.1. It is assumed that  is allowed to undergo
rigid-body transformations and will therefore have its own part
configuration space,
is allowed to undergo
rigid-body transformations and will therefore have its own part
configuration space,
 or
or
 . Let
. Let
 denote a part configuration. The transformed part model
is denoted as
denote a part configuration. The transformed part model
is denoted as
 .
.
Figure 7.15:
Examples of several important subsets of
 for manipulation planning.
for manipulation planning.
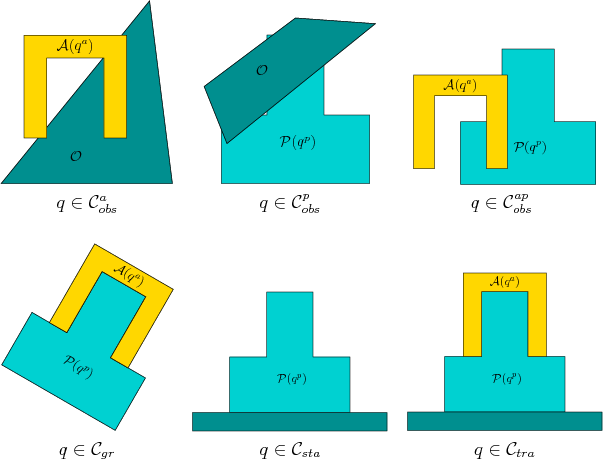 |
The combined configuration space,  , is defined as the
Cartesian product
, is defined as the
Cartesian product
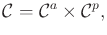 |
(7.14) |
in which each configuration
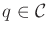 is of the form
is of the form
 .
The first step is to remove all configurations that must be avoided.
Parts of Figure 7.15 show examples of these sets.
Configurations for which the manipulator collides with obstacles are
.
The first step is to remove all configurations that must be avoided.
Parts of Figure 7.15 show examples of these sets.
Configurations for which the manipulator collides with obstacles are
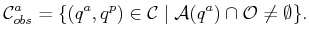 |
(7.15) |
The next logical step is to remove configurations for which the part
collides with obstacles. It will make sense to allow the part to
``touch'' the obstacles. For example, this could model a part sitting
on a table. Therefore, let
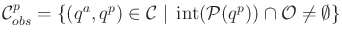 |
(7.16) |
denote the open set for which the interior of the part intersects
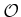 . Certainly, if the part penetrates
. Certainly, if the part penetrates 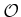 , then the configuration
should be avoided.
, then the configuration
should be avoided.
Consider
 . The configurations that
remain ensure that the robot and part do not inappropriately collide
with
. The configurations that
remain ensure that the robot and part do not inappropriately collide
with 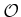 . Next consider the interaction between
. Next consider the interaction between 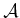 and
and 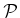 . The
manipulator must be allowed to touch the part, but penetration is once
again not allowed. Therefore, let
. The
manipulator must be allowed to touch the part, but penetration is once
again not allowed. Therefore, let
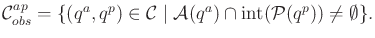 |
(7.17) |
Removing all of these bad configurations yields
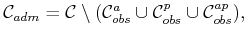 |
(7.18) |
which is called the set of admissible configurations.
Steven M LaValle
2020-08-14

![]() , is defined as the
Cartesian product
, is defined as the
Cartesian product
![]() . The configurations that
remain ensure that the robot and part do not inappropriately collide
with
. The configurations that
remain ensure that the robot and part do not inappropriately collide
with ![]() . Next consider the interaction between
. Next consider the interaction between ![]() and
and ![]() . The
manipulator must be allowed to touch the part, but penetration is once
again not allowed. Therefore, let
. The
manipulator must be allowed to touch the part, but penetration is once
again not allowed. Therefore, let