- Consider the set
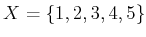 . Let
. Let  ,
, 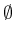 ,
,
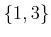 ,
, 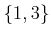 ,
, 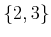 ,
, 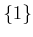 ,
, 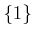 , and
, and 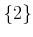 be the
collection of all subsets of
be the
collection of all subsets of  that are designated as open
sets.
that are designated as open
sets.
- Is
 a topological space?
a topological space?
- Is it a topological space if
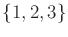 is added to the
collection of open sets? Explain.
is added to the
collection of open sets? Explain.
- What are the closed sets (assuming
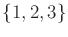 is included as an
open set)?
is included as an
open set)?
- Are any subsets of
 neither open nor closed?
neither open nor closed?
- Continuous functions for the strange topology:
- Give an example of a continuous function,
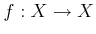 ,
for the strange topology in Example 4.4.
,
for the strange topology in Example 4.4.
- Characterize the set of all possible continuous functions.
- For the letters of the Russian alphabet, A, B, V, G, D, E,
Ë, Zh, Z, I, uI, K, L, M, N, O, P, R, S, T, U, F, H, Ts, Ch, Sh,
Shch, , Y, , E1, Yu, Ya, determine which pairs are
homeomorphic. Imagine each as a 1D subset of
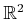 and draw them accordingly before solving the problem.
and draw them accordingly before solving the problem.
- Prove that homeomorphisms yield an equivalence relation on
the collection of all topological spaces.
- What is the dimension of the C-space for a cylindrical rod that
can translate and rotate in
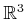 ? If the rod is rotated about its
central axis, it is assumed that the rod's position and orientation
are not changed in any detectable way. Express the C-space of the rod
in terms of a Cartesian product of simpler spaces (such as
? If the rod is rotated about its
central axis, it is assumed that the rod's position and orientation
are not changed in any detectable way. Express the C-space of the rod
in terms of a Cartesian product of simpler spaces (such as
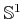 ,
,
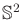 ,
,
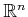 ,
, 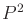 , etc.). What is your reasoning?
, etc.). What is your reasoning?
- Let
![$ \tau_1 : [0,1] \rightarrow {\mathbb{R}}^2$](img1650.gif) be a loop path that
traverses the unit circle in the plane, defined as
be a loop path that
traverses the unit circle in the plane, defined as
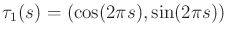 . Let
. Let
![$ \tau_2 : [0,1] \rightarrow
{\mathbb{R}}^2$](img1652.gif) be another loop path:
be another loop path:
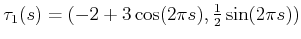 . This path traverses an ellipse that is
centered at
. This path traverses an ellipse that is
centered at 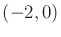 . Show that
. Show that 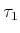 and
and 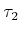 are homotopic
(by constructing a continuous function with an additional parameter
that ``morphs''
are homotopic
(by constructing a continuous function with an additional parameter
that ``morphs'' 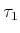 into
into 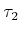 ).
).
- Prove that homotopy yields an equivalence relation on the set of
all paths from some
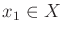 to some
to some 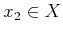 , in which
, in which 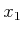 and
and 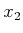 may be chosen arbitrarily.
may be chosen arbitrarily.
- Determine the C-space for a spacecraft that can translate and
rotate in a 2D Asteroids-style video game. The sides of the screen
are identified. The top and bottom are also identified. There are no
``twists'' in the identifications.
- Repeat the derivation of
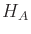 from Section 4.3.3,
but instead consider Type VE contacts.
from Section 4.3.3,
but instead consider Type VE contacts.
- Determine the C-space for a car that drives around on a huge
sphere (such as the earth with no mountains or oceans). Assume the
sphere is big enough so that its curvature may be neglected (e.g., the
car rests flatly on the earth without wobbling). [Hint: It is not
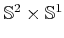 .]
.]
- Suppose that
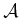 and
and 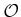 are each defined as equilateral
triangles, with coordinates
are each defined as equilateral
triangles, with coordinates 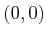 ,
, 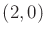 , and
, and
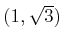 .
Determine the C-space obstacle. Specify the coordinates of all of its
vertices and indicate the corresponding contact type for each edge.
.
Determine the C-space obstacle. Specify the coordinates of all of its
vertices and indicate the corresponding contact type for each edge.
- Show that (4.20) is a valid rotation matrix for all
unit quaternions.
- Show that
![$ {\mathbb{F}}[x_1,\ldots, x_n]$](img1515.gif) , the set of polynomials over a
field
, the set of polynomials over a
field
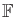 with variables
with variables
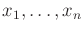 , is a group with respect to
addition.
, is a group with respect to
addition.
- Quaternions:
- Define a unit quaternion
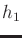 that expresses a rotation of
that expresses a rotation of
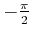 around the axis given by the vector
around the axis given by the vector
![$ [ \frac{1}{\sqrt
3} \;\; \frac{1}{\sqrt 3} \;\; \frac{1}{\sqrt 3} ]$](img1660.gif) .
.
- Define a unit quaternion
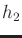 that expresses a rotation of
that expresses a rotation of
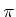 around the axis given by the vector
around the axis given by the vector
![$ [ 0 \;\; 1 \;\; 0 ]$](img1662.gif) .
.
- Suppose the rotation represented by
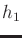 is performed, followed
by the rotation represented by
is performed, followed
by the rotation represented by 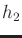 . This combination of rotations
can be represented as a single rotation around an axis given by a
vector. Find this axis and the angle of rotation about this axis.
. This combination of rotations
can be represented as a single rotation around an axis given by a
vector. Find this axis and the angle of rotation about this axis.
- What topological space is contributed to the C-space by a
spherical joint that achieves any orientation except the identity?
- Suppose five polyhedral bodies float freely in a 3D world. They
are each capable of rotating and translating. If these are treated as
``one'' composite robot, what is the topology of the resulting C-space
(assume that the bodies are not attached to each other)? What
is its dimension?
- Suppose a goal region
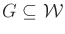 is defined in the
C-space by requiring that the entire robot is contained in
is defined in the
C-space by requiring that the entire robot is contained in 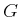 .
For example, a car may have to be parked entirely within a space in a
parking lot.
.
For example, a car may have to be parked entirely within a space in a
parking lot.
- Give a definition of
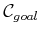 that is similar to
(4.34) but pertains to containment of
that is similar to
(4.34) but pertains to containment of 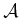 inside of
inside of
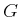 .
.
- For the case in which
 and
and  are convex and polygonal,
develop an algorithm for efficiently computing
are convex and polygonal,
develop an algorithm for efficiently computing
 .
.
- Figure 4.29a shows the Möbius band defined by
identification of sides of the unit square. Imagine that scissors are
used to cut the band along the two dashed lines. Describe the
resulting topological space. Is it a manifold? Explain.
Figure 4.29:
(a) What topological space is obtained
after slicing the Möbius band? (b) Is a manifold obtained after
tearing holes out of the plane?
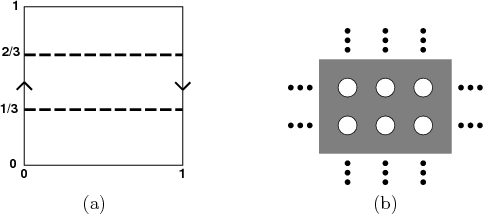 |
- Consider Figure 4.29b, which shows the set of points
in
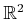 that are remaining after a closed disc of radius
that are remaining after a closed disc of radius 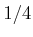 with
center
with
center 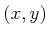 is removed for every value of
is removed for every value of 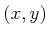 such that
such that 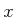 and
and
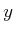 are both integers.
are both integers.
- Is the remaining set of points a manifold? Explain.
- Now remove discs of radius
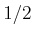 instead of
instead of 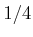 . Is a
manifold obtained?
. Is a
manifold obtained?
- Finally, remove disks of radius
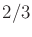 . Is a manifold
obtained?
. Is a manifold
obtained?
- Show that the solution curves shown in Figure 4.26
correctly illustrate the variety given in (4.73).
- Find the number of faces of
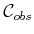 for a cube and regular
tetrahedron, assuming
for a cube and regular
tetrahedron, assuming 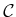 is
is 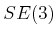 . How many faces of each contact
type are obtained?
. How many faces of each contact
type are obtained?
- Following the analysis matrix subgroups from Section
4.2, determine the dimension of
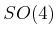 , the group of
, the group of
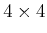 rotation matrices. Can you characterize this topological
space?
rotation matrices. Can you characterize this topological
space?
- Suppose that a kinematic chain of spherical joints is given.
Show how to use (4.20) as the rotation part in each
homogeneous transformation matrix, as opposed to using the DH
parameterization. Explain why using (4.20) would be
preferable for motion planning applications.
- Suppose that the constraint that
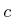 is held to position
is held to position
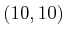 is imposed on the mechanism shown in Figure
3.29. Using complex numbers to represent rotation,
express this constraint using polynomial equations.
is imposed on the mechanism shown in Figure
3.29. Using complex numbers to represent rotation,
express this constraint using polynomial equations.
- The Tangle toy is made of
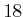 pieces of macaroni-shaped joints
that are attached together to form a loop. Each attachment between
joints forms a revolute joint. Each link is a curved tube that
extends around
pieces of macaroni-shaped joints
that are attached together to form a loop. Each attachment between
joints forms a revolute joint. Each link is a curved tube that
extends around 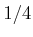 of a circle. What is the dimension of the
variety that results from maintaining the loop? What is its
configuration space (accounting for internal degrees of freedom),
assuming the toy can be placed anywhere in
of a circle. What is the dimension of the
variety that results from maintaining the loop? What is its
configuration space (accounting for internal degrees of freedom),
assuming the toy can be placed anywhere in
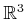 ?
?
Implementations
- Computing C-space obstacles:
- Implement the algorithm from Section 4.3.2 to
construct a convex, polygonal C-space obstacle.
- Now allow the robot to rotate in the plane. For any convex robot
and obstacle, compute the orientations at which the C-space obstacle
fundamentally changes due to different Type EV and Type VE
contacts becoming
active.
- Animate the changing C-space obstacle by using the robot
orientation as the time axis in the animation.
- Consider ``straight-line'' paths that start at the origin (lower
left corner) of the manifolds shown in Figure 4.5
and leave at a particular angle, which is input to the program. The
lines must respect identifications; thus, as the line hits the edge of
the square, it may continue onward. Study the conditions under which
the lines fill the entire space versus forming a finite pattern (i.e.,
a segment, stripes, or a tiling).
Steven M LaValle
2020-08-14

