
Next: 3D rigid bodies Up: 4.3 Configuration Space Obstacles Previous: A polyhedral C-space obstacle
Unfortunately, the cases in which
![]() is polygonal or polyhedral
are quite limited. Most problems yield extremely complicated C-space
obstacles. One good point is that
is polygonal or polyhedral
are quite limited. Most problems yield extremely complicated C-space
obstacles. One good point is that
![]() can be expressed using
semi-algebraic models, for any robots and obstacles defined using
semi-algebraic models, even after applying any of the transformations
from Sections 3.2 to 3.4. It might not be
true, however, for other kinds of transformations, such as warping a
flexible material [32,577].
can be expressed using
semi-algebraic models, for any robots and obstacles defined using
semi-algebraic models, even after applying any of the transformations
from Sections 3.2 to 3.4. It might not be
true, however, for other kinds of transformations, such as warping a
flexible material [32,577].
Consider the case of a convex polygonal robot and a convex polygonal
obstacle in a 2D world. Assume that any transformation in ![]() may
be applied to
may
be applied to ![]() ; thus,
; thus,
![]() and
and
![]() . The task is to define a set of algebraic
primitives that can be combined to define
. The task is to define a set of algebraic
primitives that can be combined to define
![]() . Once again, it is important to distinguish between Type
EV and Type VE contacts.
Consider how to construct the algebraic primitives for the Type EV contacts; Type VE can be handled in a
similar manner.
. Once again, it is important to distinguish between Type
EV and Type VE contacts.
Consider how to construct the algebraic primitives for the Type EV contacts; Type VE can be handled in a
similar manner.
For the translation-only case, we were able to determine all of the
Type EV contacts by sorting the edge normals.
With rotation, the ordering of edge normals depends on ![]() . This
implies that the applicability of a Type EV
contact depends on
. This
implies that the applicability of a Type EV
contact depends on ![]() , the robot orientation. Recall the
constraint that the inward normal of
, the robot orientation. Recall the
constraint that the inward normal of ![]() must point between the
outward normals of the edges of
must point between the
outward normals of the edges of ![]() that contain the vertex of
contact, as shown in Figure 4.21. This constraint can be
expressed in terms of inner products using the vectors
that contain the vertex of
contact, as shown in Figure 4.21. This constraint can be
expressed in terms of inner products using the vectors ![]() and
and
![]() . The statement regarding the directions of the normals can
equivalently be formulated as the statement that the angle between
. The statement regarding the directions of the normals can
equivalently be formulated as the statement that the angle between ![]() and
and ![]() , and between
, and between ![]() and
and ![]() , must each be less than
, must each be less than ![]() .
Using inner products, this implies that
.
Using inner products, this implies that
![]() and
and
![]() . As in the translation case, the condition
. As in the translation case, the condition
![]() is required for contact. Observe that
is required for contact. Observe that ![]() now depends on
now depends on
![]() . For any
. For any
![]() , if
, if
![]() ,
,
![]() , and
, and
![]() , then
, then
![]() . Let
. Let ![]() denote the set of configurations that satisfy
these conditions. These conditions imply that a point is in
denote the set of configurations that satisfy
these conditions. These conditions imply that a point is in
![]() .
Furthermore, any other Type EV and Type
VE contacts could imply that more points are in
.
Furthermore, any other Type EV and Type
VE contacts could imply that more points are in
![]() . Ordinarily,
. Ordinarily,
![]() , which implies that the
complement,
, which implies that the
complement,
![]() , is a superset of
, is a superset of
![]() (thus,
(thus,
![]() ). Let
). Let
![]() . Using the
primitives
. Using the
primitives
| (4.39) |
| (4.40) |
| (4.41) |
It is known that
![]() , but
, but ![]() may contain points
in
may contain points
in
![]() . The situation is similar to what was explained in
Section 3.1.1 for building a model of a convex polygon
from half-planes. In the current setting, it is only known that any
configuration outside of
. The situation is similar to what was explained in
Section 3.1.1 for building a model of a convex polygon
from half-planes. In the current setting, it is only known that any
configuration outside of ![]() must be in
must be in
![]() . If
. If ![]() is
intersected with all other corresponding sets for each possible Type
EV and Type VE contact,
then the result is
is
intersected with all other corresponding sets for each possible Type
EV and Type VE contact,
then the result is
![]() . Each contact has the opportunity to
remove a portion of
. Each contact has the opportunity to
remove a portion of
![]() from consideration. Eventually, enough
pieces of
from consideration. Eventually, enough
pieces of
![]() are removed so that the only configurations
remaining must lie in
are removed so that the only configurations
remaining must lie in
![]() . For any Type EV contact,
. For any Type EV contact,
![]() . A similar statement can be
made for Type VE contacts. A logical
predicate, similar to that defined in Section 3.1.1, can
be constructed to determine whether
. A similar statement can be
made for Type VE contacts. A logical
predicate, similar to that defined in Section 3.1.1, can
be constructed to determine whether
![]() in time that is
linear in the number of
in time that is
linear in the number of
![]() primitives.
primitives.
One important issue remains. The expression ![]() is not a
polynomial because of the
is not a
polynomial because of the
![]() and
and
![]() terms in the
rotation matrix of
terms in the
rotation matrix of ![]() . If polynomials could be substituted for
these expressions, then everything would be fixed because the
expression of the normal vector (not a unit normal) and the inner
product are both linear functions, thereby transforming polynomials
into polynomials. Such a substitution can be made using stereographic
projection (see [588]); however, a simpler approach is to use
complex numbers to represent rotation. Recall that when
. If polynomials could be substituted for
these expressions, then everything would be fixed because the
expression of the normal vector (not a unit normal) and the inner
product are both linear functions, thereby transforming polynomials
into polynomials. Such a substitution can be made using stereographic
projection (see [588]); however, a simpler approach is to use
complex numbers to represent rotation. Recall that when ![]() is
used to represent rotation, each rotation matrix in
is
used to represent rotation, each rotation matrix in ![]() is
represented as (4.18), and the
is
represented as (4.18), and the
![]() homogeneous transformation matrix becomes
homogeneous transformation matrix becomes
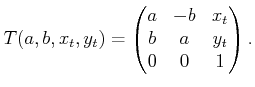 |
(4.42) |
This was a simple trick to make a nice, linear function, but what was
the cost? The dependency is now on ![]() and
and ![]() instead of
instead of ![]() .
This appears to increase the dimension of
.
This appears to increase the dimension of ![]() from 3 to 4, and
from 3 to 4, and
![]() . However, an algebraic primitive
must be added that constrains
. However, an algebraic primitive
must be added that constrains ![]() and
and ![]() to lie on the unit circle.
to lie on the unit circle.
By using complex numbers, primitives in
![]() are obtained for each
Type EV and Type VE
contact. By defining
are obtained for each
Type EV and Type VE
contact. By defining
![]() , the following algebraic
primitives are obtained for a Type EV
contact:
, the following algebraic
primitives are obtained for a Type EV
contact:
| (4.43) |
| (4.44) |
| (4.45) |
| (4.46) |
One interesting observation can be made here. The only nonlinear
primitive is
![]() . Therefore,
. Therefore,
![]() can be considered as
a linear polytope (like a polyhedron, but one dimension higher) in
can be considered as
a linear polytope (like a polyhedron, but one dimension higher) in
![]() that is intersected with a cylinder.
that is intersected with a cylinder.
![]()