For a given field
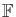 and positive integer
and positive integer  , the
, the  -dimensional
affine space over
-dimensional
affine space over
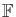 is the set
is the set
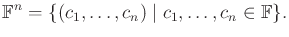 |
(4.51) |
For our purposes in this section, an affine space can be considered as
a vector space (for an exact definition, see [438]). Thus,
 is like a vector version of the scalar field
is like a vector version of the scalar field
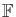 . Familiar
examples of this are
. Familiar
examples of this are
 ,
,
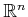 , and
, and
 .
.
A polynomial in
![$ f \in {\mathbb{F}}[x_1,\ldots,x_n]$](img1527.gif) can be converted into
a function,
can be converted into
a function,
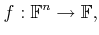 |
(4.52) |
by substituting elements of
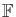 for each variable and evaluating the
expression using the field operations. This can be written as
for each variable and evaluating the
expression using the field operations. This can be written as
 , in which each
, in which each 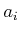 denotes an element of
denotes an element of
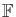 that is substituted for the variable
that is substituted for the variable 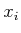 .
.
We now arrive at an interesting question. For a given 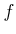 , what are
the elements of
, what are
the elements of
 such that
such that
 ? We could
also ask the question for some nonzero element, but notice that this
is not necessary because the polynomial may be redefined to formulate
the question using 0. For example, what are the elements of
? We could
also ask the question for some nonzero element, but notice that this
is not necessary because the polynomial may be redefined to formulate
the question using 0. For example, what are the elements of
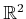 such that
such that
 ? This familiar equation for
? This familiar equation for
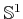 can be
reformulated to yield: What are the elements of
can be
reformulated to yield: What are the elements of
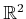 such that
such that
 ?
?
Let
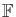 be a field and let
be a field and let
 be a set of
polynomials in
be a set of
polynomials in
![$ {\mathbb{F}}[x_1,\ldots, x_n]$](img1515.gif) . The set
. The set
 for all for all 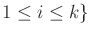 |
(4.53) |
is called the (affine) variety defined by
 . One interesting fact is that unions and
intersections of varieties are varieties. Therefore, they behave like
the semi-algebraic sets from Section 3.1.2, but for
varieties only equality constraints are allowed. Consider the
varieties
. One interesting fact is that unions and
intersections of varieties are varieties. Therefore, they behave like
the semi-algebraic sets from Section 3.1.2, but for
varieties only equality constraints are allowed. Consider the
varieties
 and
and
 . Their
intersection is given by
. Their
intersection is given by
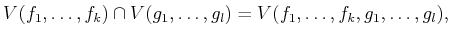 |
(4.54) |
because each element of
 must produce a 0 value for each of
the polynomials in
must produce a 0 value for each of
the polynomials in
 .
.
To obtain unions, the polynomials simply need to be multiplied. For
example, consider the varieties
 defined as
defined as
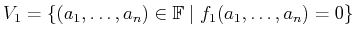 |
(4.55) |
and
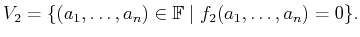 |
(4.56) |
The set
 is obtained by forming the
polynomial
is obtained by forming the
polynomial
 . Note that
. Note that
 if either
if either
 or
or
 . Therefore,
. Therefore,
 is a variety. The varieties
is a variety. The varieties  and
and  were
defined using a single polynomial, but the same idea applies to any
variety. All pairs of the form
were
defined using a single polynomial, but the same idea applies to any
variety. All pairs of the form  must appear in the argument
of
must appear in the argument
of  if there are multiple polynomials.
if there are multiple polynomials.
Steven M LaValle
2020-08-14

![]() and positive integer
and positive integer ![]() , the
, the ![]() -dimensional
affine space over
-dimensional
affine space over
![]() is the set
is the set
![]() can be converted into
a function,
can be converted into
a function,
![]() , what are
the elements of
, what are
the elements of
![]() such that
such that
![]() ? We could
also ask the question for some nonzero element, but notice that this
is not necessary because the polynomial may be redefined to formulate
the question using 0. For example, what are the elements of
? We could
also ask the question for some nonzero element, but notice that this
is not necessary because the polynomial may be redefined to formulate
the question using 0. For example, what are the elements of
![]() such that
such that
![]() ? This familiar equation for
? This familiar equation for
![]() can be
reformulated to yield: What are the elements of
can be
reformulated to yield: What are the elements of
![]() such that
such that
![]() ?
?
![]() be a field and let
be a field and let
![]() be a set of
polynomials in
be a set of
polynomials in
![]() . The set
. The set
![]() defined as
defined as