
Next: Special Euclidean group Up: 4.2.2 3D Rigid Bodies: Previous: Using quaternion multiplication
Recall from Section 3.2.3 that given a rotation matrix
(3.43), the yaw, pitch, and roll parameters could be directly
determined using the ![]() function. It turns out that the
quaternion representation can also be determined directly from the
matrix. This is the inverse of the function in
(4.20).4.9
function. It turns out that the
quaternion representation can also be determined directly from the
matrix. This is the inverse of the function in
(4.20).4.9
For a given rotation matrix (3.43), the quaternion
parameters
![]() can be computed as follows
[210]. The first component is
can be computed as follows
[210]. The first component is
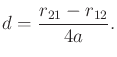 |
(4.27) |
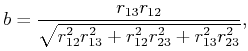 |
(4.28) |
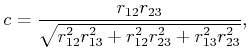 |
(4.29) |
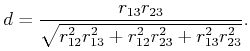 |
(4.30) |
Steven M LaValle 2020-08-14