A 3D body can be rotated about three orthogonal axes, as shown in
Figure 3.8. Borrowing aviation terminology, these
rotations will be referred to as yaw, pitch, and roll:
- A yaw is a counterclockwise rotation
of
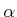 about the
about the 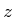 -axis. The rotation matrix is given by
-axis. The rotation matrix is given by
 |
(3.39) |
Note that the upper left entries of
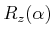 form a 2D rotation
applied to the
form a 2D rotation
applied to the 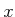 and
and 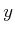 coordinates, whereas the
coordinates, whereas the 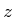 coordinate
remains constant.
coordinate
remains constant.
- A pitch is a counterclockwise
rotation of
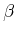 about the
about the 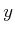 -axis. The rotation matrix is given
by
-axis. The rotation matrix is given
by
 |
(3.40) |
- A roll is a counterclockwise rotation
of
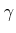 about the
about the 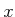 -axis. The rotation matrix is given by
-axis. The rotation matrix is given by
 |
(3.41) |
Each rotation matrix is a simple extension of the 2D rotation matrix,
(3.31). For example, the yaw matrix,
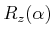 ,
essentially performs a 2D rotation with respect to the
,
essentially performs a 2D rotation with respect to the 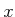 and
and 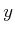 coordinates while leaving the
coordinates while leaving the 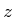 coordinate unchanged. Thus, the
third row and third column of
coordinate unchanged. Thus, the
third row and third column of
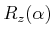 look like part of the
identity matrix, while the upper right portion of
look like part of the
identity matrix, while the upper right portion of
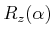 looks
like the 2D rotation matrix.
looks
like the 2D rotation matrix.
The yaw, pitch, and roll rotations can be used to place a 3D body in
any orientation. A single rotation matrix can be formed by
multiplying the yaw, pitch, and roll rotation matrices to obtain
 |
(3.42) |
It is important to note that
 performs the
roll first, then the pitch, and finally the yaw. If the order of
these operations is changed, a different rotation matrix would result.
Be careful when interpreting the rotations. Consider the final
rotation, a yaw by
performs the
roll first, then the pitch, and finally the yaw. If the order of
these operations is changed, a different rotation matrix would result.
Be careful when interpreting the rotations. Consider the final
rotation, a yaw by 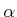 . Imagine sitting inside of a robot
. Imagine sitting inside of a robot  that looks like an aircraft. If
that looks like an aircraft. If
 , then the yaw
turns the plane in a way that feels like turning a car to the left.
However, for arbitrary values of
, then the yaw
turns the plane in a way that feels like turning a car to the left.
However, for arbitrary values of 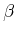 and
and 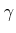 , the final
rotation axis will not be vertically aligned with the aircraft because
the aircraft is left in an unusual orientation before
, the final
rotation axis will not be vertically aligned with the aircraft because
the aircraft is left in an unusual orientation before 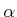 is
applied. The yaw rotation occurs about the
is
applied. The yaw rotation occurs about the 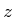 -axis of the world
frame, not the body frame of
-axis of the world
frame, not the body frame of 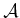 . Each time a new rotation matrix is
introduced from the left, it has no concern for original body frame of
. Each time a new rotation matrix is
introduced from the left, it has no concern for original body frame of
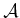 . It simply rotates every point in
. It simply rotates every point in
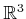 in terms of the world
frame. Note that 3D rotations depend on three parameters,
in terms of the world
frame. Note that 3D rotations depend on three parameters, 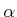 ,
,
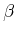 , and
, and 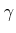 , whereas 2D rotations depend only on a single
parameter,
, whereas 2D rotations depend only on a single
parameter, 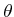 . The primitives of the model can be transformed
using
. The primitives of the model can be transformed
using
 , resulting in
, resulting in
 .
.
Steven M LaValle
2020-08-14
