
Next: Approximation algorithm framework Up: 14.4.1.2 Extensions and other Previous: Multiple, independent double integrators
A lattice can even be obtained for the general case of a fully
actuated mechanical system, which for example includes most robot
arms. Recall from (13.4) that any system in the form
![]() can alternatively be expressed as
can alternatively be expressed as
![]() , if
, if
![]() is defined as the image of
is defined as the image of ![]() for a fixed
for a fixed ![]() . The main
purpose of using
. The main
purpose of using ![]() is to make it easy to specify a fixed action
space
is to make it easy to specify a fixed action
space ![]() that maps differently into the tangent space for each
that maps differently into the tangent space for each
![]() .
.
A similar observation can be made regarding equations of the form
![]() , in which
, in which ![]() and
and ![]() is an open subset
of
is an open subset
of
![]() . Recall that this form was obtained for general
unconstrained mechanical systems in Sections 13.3 and
13.4. For example, (13.148) expresses the
dynamics of open-chain robot arms. Such equations can be expressed as
. Recall that this form was obtained for general
unconstrained mechanical systems in Sections 13.3 and
13.4. For example, (13.148) expresses the
dynamics of open-chain robot arms. Such equations can be expressed as
![]() by directly specifying the set of allowable
accelerations. Each
by directly specifying the set of allowable
accelerations. Each ![]() will map to a new action
will map to a new action ![]() in an action
space given by
in an action
space given by
Each
![]() directly expresses an acceleration vector in
directly expresses an acceleration vector in
![]() . Therefore, using
. Therefore, using
![]() , the original equation
expressed using
, the original equation
expressed using ![]() can be now written as
can be now written as
![]() . In its new
form, this appears just like the multiple, independent double
integrators. The main differences are
. In its new
form, this appears just like the multiple, independent double
integrators. The main differences are
 |
The first difference is handled by performing grid sampling over
![]() and making an edge in the reachability graph for every grid
point that falls into
and making an edge in the reachability graph for every grid
point that falls into
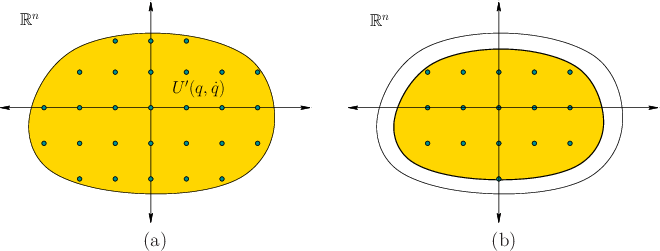
![]() ; see Figure 14.15a.
The grid resolution can be improved along with
; see Figure 14.15a.
The grid resolution can be improved along with ![]() to obtain
resolution completeness. To address the second problem, think of
to obtain
resolution completeness. To address the second problem, think of
![]() as a shape in
as a shape in
![]() that moves over time.
Choosing
that moves over time.
Choosing ![]() close to the boundary of
close to the boundary of
![]() is
dangerous because as
is
dangerous because as ![]() increases,
increases, ![]() may fall outside of the new
action set. It is often possible to obtain bounds on how quickly the
boundary of
may fall outside of the new
action set. It is often possible to obtain bounds on how quickly the
boundary of
![]() can vary over time (this can be determined,
for example, by differentiating
can vary over time (this can be determined,
for example, by differentiating ![]() with respect to
with respect to ![]() and
and ![]() ).
Based on the bound, a thin layer near the boundary of
).
Based on the bound, a thin layer near the boundary of
![]() can be removed from consideration to ensure that all attempted actions
remain in
can be removed from consideration to ensure that all attempted actions
remain in
![]() during the whole interval
during the whole interval ![]() .
See Figure 14.15b.
.
See Figure 14.15b.
These ideas were applied to extend the approximation algorithm
framework to the case of open-chain robot arms, for which ![]() is given
by (13.148). Suppose that
is given
by (13.148). Suppose that ![]() is an axis-aligned
rectangle, which is often the case for manipulators because the bounds
for each
is an axis-aligned
rectangle, which is often the case for manipulators because the bounds
for each ![]() correspond to torque limits for each motor. If
correspond to torque limits for each motor. If ![]() and
and
![]() are fixed, then (13.140) applies a linear
transformation to obtain
are fixed, then (13.140) applies a linear
transformation to obtain ![]() from
from ![]() . The rectangle is
generally sheared into a parallelepiped (a
. The rectangle is
generally sheared into a parallelepiped (a ![]() -dimensional extension
of a parallelogram). Recall such transformations from Section
3.5 or linear algebra.
-dimensional extension
of a parallelogram). Recall such transformations from Section
3.5 or linear algebra.
Steven M LaValle 2020-08-14