The lattices developed in this section were introduced in
[290] for analyzing the kinodynamic planning problem
in the rigorous approximation algorithm framework for NP-hard
problems [765]. Suppose that there are two or three
independent double integrators. The analysis shows that the computed
solutions are approximately optimal in the following sense. Let 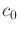 and
and 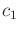 be two positive constants that define a function
be two positive constants that define a function
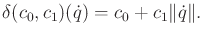 |
(14.25) |
Let 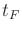 denote the time at which the termination action is applied.
A state trajectory is called
denote the time at which the termination action is applied.
A state trajectory is called
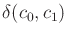 -safe if for all
-safe if for all
![$ t \in [0,t_F]$](img6364.gif) , the ball of radius
, the ball of radius
 that is
centered at
that is
centered at 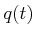 does not cause collisions with obstacles in
does not cause collisions with obstacles in 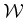 .
Note that the ball radius grows linearly as the speed increases. The
robot can be imagined as a disk with a radius determined by speed.
Let
.
Note that the ball radius grows linearly as the speed increases. The
robot can be imagined as a disk with a radius determined by speed.
Let 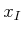 ,
, 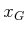 ,
, 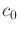 , and
, and 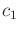 be given (only a point goal
region is allowed). Suppose that for a given problem, there exists a
be given (only a point goal
region is allowed). Suppose that for a given problem, there exists a
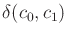 -safe state trajectory (resulting from integrating
any
-safe state trajectory (resulting from integrating
any
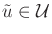 ) that terminates in
) that terminates in 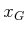 after time
after time 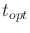 .
It was shown that by choosing the appropriate
.
It was shown that by choosing the appropriate 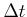 (given by a
formula in [290]), applying breadth-first search to
the reachability lattice will find a
(given by a
formula in [290]), applying breadth-first search to
the reachability lattice will find a
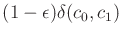 -safe trajectory that takes time at most
-safe trajectory that takes time at most
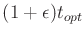 , and approximately connects
, and approximately connects 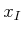 to
to
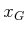 (which means that the closeness in
(which means that the closeness in  depends on
depends on
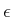 ). Furthermore, the running time of the algorithm is
polynomial in
). Furthermore, the running time of the algorithm is
polynomial in
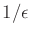 and the number of primitives used to define
polygonal obstacles.14.5 One of the key steps in the analysis is to show that any state
trajectory can be closely tracked using only actions from
and the number of primitives used to define
polygonal obstacles.14.5 One of the key steps in the analysis is to show that any state
trajectory can be closely tracked using only actions from 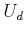 and
keeping them constant over
and
keeping them constant over 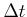 . One important aspect is that
it does not necessarily imply that the computed solution is close to
the true optimum, as it travels through
. One important aspect is that
it does not necessarily imply that the computed solution is close to
the true optimum, as it travels through  (only the execution times
are close). Thus, the algorithm may give a solution from a different
homotopy class from the one that contains the true optimal trajectory.
The analysis was extended to the general case of open-chain robot arms
in [288,441].
(only the execution times
are close). Thus, the algorithm may give a solution from a different
homotopy class from the one that contains the true optimal trajectory.
The analysis was extended to the general case of open-chain robot arms
in [288,441].
Steven M LaValle
2020-08-14

![]() and
and ![]() be two positive constants that define a function
be two positive constants that define a function