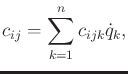13.4.2 General Lagrangian Expressions
As more complicated mechanics problems are considered, it is
convenient to express the differential constraints in a general form.
For example, evaluating (13.130) for a kinematic chain of
bodies leads to very complicated expressions. The terms of these
expressions, however, can be organized into standard forms that appear
simpler and give some intuitive meanings to the components.
Suppose that the kinetic energy is expressed using (13.126),
and let 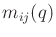 denote an entry of
denote an entry of 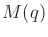 . Suppose that the
potential energy is
. Suppose that the
potential energy is 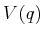 . By performing the derivatives expressed
in (13.136), the Euler-Lagrange equation can be expressed as
. By performing the derivatives expressed
in (13.136), the Euler-Lagrange equation can be expressed as
 scalar equations of the form [856]
scalar equations of the form [856]
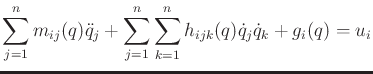 |
(13.140) |
in which
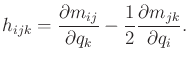 |
(13.141) |
There is one equation for each 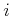 from
from 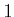 to
to  . The components of
(13.140) have physical interpretations. The
. The components of
(13.140) have physical interpretations. The 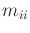 coefficients represent the inertia with respect to
coefficients represent the inertia with respect to 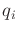 . The
. The
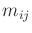 represent the affect on
represent the affect on 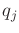 of accelerating
of accelerating 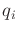 . The
. The
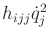 terms represent the centrifugal effect induced on
terms represent the centrifugal effect induced on
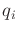 by the velocity of
by the velocity of 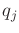 . The
. The
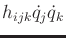 terms
represent the Coriolis effect induced on
terms
represent the Coriolis effect induced on 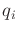 by the velocities of
by the velocities of
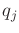 and
and 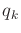 . The
. The 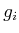 term usually arises from gravity.
term usually arises from gravity.
An alternative to (13.140) is often given in terms of
matrices. It can be shown that the Euler-Lagrange equation
reduces to
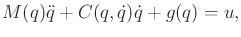 |
(13.142) |
which represents  scalar equations. This introduces
scalar equations. This introduces
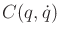 ,
which is an
,
which is an
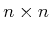 Coriolis matrix. It turns out that
many possible Coriolis matrices may produce equivalent different
constraints. With respect to (13.140), the Coriolis
matrix must be chosen so that
Coriolis matrix. It turns out that
many possible Coriolis matrices may produce equivalent different
constraints. With respect to (13.140), the Coriolis
matrix must be chosen so that
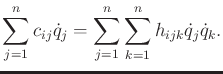 |
(13.143) |
Using (13.141),
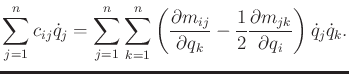 |
(13.144) |
A standard way to determine
 is by computing Christoffel symbols. By subtracting
is by computing Christoffel symbols. By subtracting
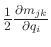 from the inside of
the nested sums in (13.144), the equation can be rewritten
as
from the inside of
the nested sums in (13.144), the equation can be rewritten
as
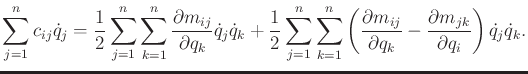 |
(13.145) |
This enables an element of
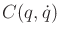 to be written as
to be written as
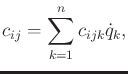 |
(13.146) |
in which
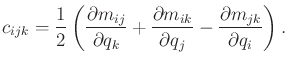 |
(13.147) |
This is called a Christoffel symbol, and it is obtained from
(13.145). Note that
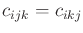 . Christoffel
symbols arise in the study of affine connections in differential
geometry and are usually denoted as
. Christoffel
symbols arise in the study of affine connections in differential
geometry and are usually denoted as
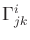 . Affine
connections provide a way to express acceleration without coordinates,
in the same way that the tangent space was expressed without
coordinates in Section 8.3.2. For affine connections in
differential geometry, see [133]; for their application to
mechanics, see [156].
. Affine
connections provide a way to express acceleration without coordinates,
in the same way that the tangent space was expressed without
coordinates in Section 8.3.2. For affine connections in
differential geometry, see [133]; for their application to
mechanics, see [156].
Subsections
Steven M LaValle
2020-08-14

![]() denote an entry of
denote an entry of ![]() . Suppose that the
potential energy is
. Suppose that the
potential energy is ![]() . By performing the derivatives expressed
in (13.136), the Euler-Lagrange equation can be expressed as
. By performing the derivatives expressed
in (13.136), the Euler-Lagrange equation can be expressed as
![]() scalar equations of the form [856]
scalar equations of the form [856]