
Next: 12.4.2 A Complete Algorithm Up: 12.4 Visibility-Based Pursuit-Evasion Previous: 12.4 Visibility-Based Pursuit-Evasion
The problem considered in this section is formulated as follows.
It will be convenient to solve the problem by verifying that there is no evader. In other words, find a path for the pursuer that upon completion guarantees that there are no remaining places where the evader could be hiding. This ensures that during execution of the plan, the pursuer will encounter any evader. In fact, there can be any number of evaders, and the pursuer will find all of them. The approach systematically eliminates any possible places where evaders could hide.
The state yields the positions of the pursuer and the evader, ![]() , which results in the state space
, which results in the state space
![]() . Since the evader position is unknown, the current state is
unknown, and I-spaces arise. The observation space
. Since the evader position is unknown, the current state is
unknown, and I-spaces arise. The observation space ![]() is a
collection of subsets of
is a
collection of subsets of ![]() . For each
. For each ![]() , the sensor yields a
visibility polygon,
, the sensor yields a
visibility polygon,
![]() (this is denoted by
(this is denoted by
![]() using notation of Section 11.1.1). Consider the
history I-state at time
using notation of Section 11.1.1). Consider the
history I-state at time ![]() . The initial pursuer position
. The initial pursuer position ![]() is
given (any position can be chosen arbitrarily, if it is not given),
and the evader may lie anywhere in
is
given (any position can be chosen arbitrarily, if it is not given),
and the evader may lie anywhere in ![]() . The input history
. The input history
![]() can be expressed as the pursuer history
can be expressed as the pursuer history
![]() .12.5 Thus, the history I-state is
.12.5 Thus, the history I-state is
| (12.33) |
Consider the nondeterministic I-space,
![]() . Since the pursuer
position is always known, the interesting part of
. Since the pursuer
position is always known, the interesting part of ![]() is the subset in
which the evader may lie. Thus, the nondeterministic I-state can be
expressed as
is the subset in
which the evader may lie. Thus, the nondeterministic I-state can be
expressed as
![]() , in which
, in which
![]() is
the set of possible evader positions given
is
the set of possible evader positions given ![]() . As usual for
nondeterministic I-states,
. As usual for
nondeterministic I-states,
![]() is the smallest set that is
consistent with all of the information in
is the smallest set that is
consistent with all of the information in ![]() .
.
Consider how
![]() varies over time. After the first instant of
time,
varies over time. After the first instant of
time, ![]() is observed, and it is known that the evader lies in
is observed, and it is known that the evader lies in
![]() , which is the shadow region (defined in Section
12.3.4) from
, which is the shadow region (defined in Section
12.3.4) from ![]() . As the pursuer moves,
. As the pursuer moves,
![]() varies.
Suppose you are told that the pursuer is now at position
varies.
Suppose you are told that the pursuer is now at position ![]() , but
you are not yet told
, but
you are not yet told ![]() . What options seem possible for
. What options seem possible for
![]() ? These depend on the history, but the only interesting
possibilities are that each shadow component may or may not contain
the evader. For some of these components, we may be certain that it
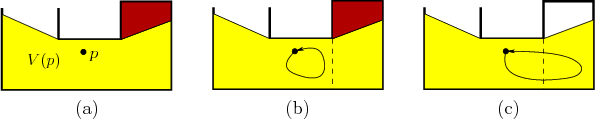
does not. For example, consider Figure 12.38. Suppose
that the pursuer initially believes that the end of the corridor may
contain the evader. If it moves along the smaller closed-loop path,
the nondeterministic I-state gradually varies but returns to the same
value when the loop is completed. However, if the pursuer traverses
the larger loop, it becomes certain upon completing the loop that the
corridor does not contain the evader. The dashed line that was
crossed in this example may inspire you to think about cell
decompositions based on critical boundaries, as in the algorithm in
Section 6.3.4. This idea will be pursued shortly to
develop a complete algorithm for solving this problem. Before
presenting a complete algorithm, however, first consider some
interesting examples.
? These depend on the history, but the only interesting
possibilities are that each shadow component may or may not contain
the evader. For some of these components, we may be certain that it
does not. For example, consider Figure 12.38. Suppose
that the pursuer initially believes that the end of the corridor may
contain the evader. If it moves along the smaller closed-loop path,
the nondeterministic I-state gradually varies but returns to the same
value when the loop is completed. However, if the pursuer traverses
the larger loop, it becomes certain upon completing the loop that the
corridor does not contain the evader. The dashed line that was
crossed in this example may inspire you to think about cell
decompositions based on critical boundaries, as in the algorithm in
Section 6.3.4. This idea will be pursued shortly to
develop a complete algorithm for solving this problem. Before
presenting a complete algorithm, however, first consider some
interesting examples.
 |
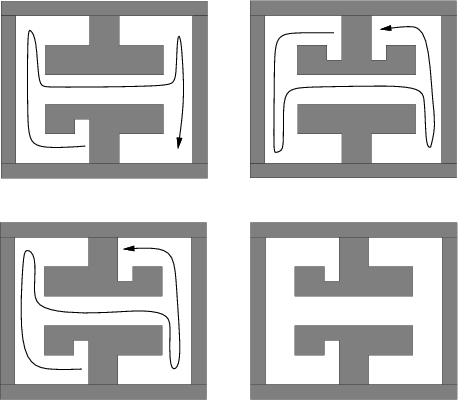 |
Since one pursuer is incapable of solving some problems, it is
tempting to wonder whether two pursuers can solve any problem. The
next example gives an interesting sequence of environments that
implies that for any positive integer ![]() , there is an environment
that requires exactly
, there is an environment
that requires exactly ![]() pursuers to solve.
pursuers to solve.
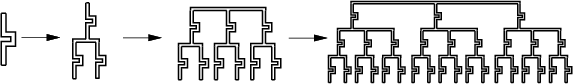 |
The problem can be made more challenging by considering multiply connected environments (environments with holes). A single pursuer cannot solve any of the these problems. Determining the minimum number of pursuers required to solve such a problem is NP-hard [414].
Steven M LaValle 2020-08-14