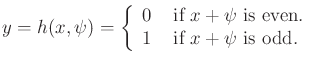11.1.1 Sensors
As the name suggests, sensors are designed to sense the state.
Throughout all of this section it is assumed that the state space,
 , is finite or countably infinite, as in Formulations 2.1
and 2.3. A sensor is defined in terms of two
components: 1) an observation space, which is the set of
possible readings for the sensor, and 2) a sensor mapping, which
characterizes the readings that can be expected if the current state
or other information is given. Be aware that in the planning model,
the state is not really given; it is only assumed to be given when
modeling a sensor. The sensing model given here generalizes the one
given in Section 9.2.3. In that case, the sensor provided
information regarding
, is finite or countably infinite, as in Formulations 2.1
and 2.3. A sensor is defined in terms of two
components: 1) an observation space, which is the set of
possible readings for the sensor, and 2) a sensor mapping, which
characterizes the readings that can be expected if the current state
or other information is given. Be aware that in the planning model,
the state is not really given; it is only assumed to be given when
modeling a sensor. The sensing model given here generalizes the one
given in Section 9.2.3. In that case, the sensor provided
information regarding  instead of
instead of  because state spaces
were not needed in Chapter 9.
because state spaces
were not needed in Chapter 9.
Let  denote an observation space, which is a finite or
countably infinite set. Let
denote an observation space, which is a finite or
countably infinite set. Let 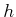 denote the sensor mapping.
Three different kinds of sensor mappings will be considered, each of
which is more complicated and general than the previous one:
denote the sensor mapping.
Three different kinds of sensor mappings will be considered, each of
which is more complicated and general than the previous one:
- State sensor mapping: In this case,
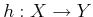 , which
means that given the state, the observation is completely determined.
, which
means that given the state, the observation is completely determined.
- State-nature sensor mapping: In this case, a finite set,
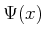 , of nature sensing actions is defined for each
, of nature sensing actions is defined for each 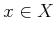 . Each nature sensing action,
. Each nature sensing action,
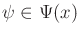 , interferes with the sensor observation.
Therefore, the state-nature mapping,
, interferes with the sensor observation.
Therefore, the state-nature mapping, 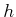 , produces an observation,
, produces an observation,
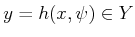 , for every
, for every 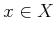 and
and
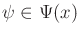 . The
particular
. The
particular 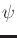 chosen by nature is assumed to be unknown during
planning and execution. However, it is specified as part of the
sensing model.
chosen by nature is assumed to be unknown during
planning and execution. However, it is specified as part of the
sensing model.
- History-based sensor mapping: In this case, the
observation could be based on the current state or any previous
states. Furthermore, a nature sensing action could be applied.
Suppose that the current stage is
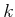 . The set of nature sensing
actions is denoted by
. The set of nature sensing
actions is denoted by 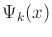 , and the particular nature sensing
action is
, and the particular nature sensing
action is
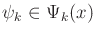 . This yields a very general sensor
mapping,
. This yields a very general sensor
mapping,
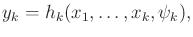 |
(11.1) |
in which 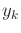 is the observation obtained in stage
is the observation obtained in stage 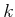 . Note that
the mapping is denoted as
. Note that
the mapping is denoted as 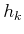 because the domain is different for
each
because the domain is different for
each 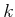 . In general, any of the sensor mappings may be
stage-dependent, if desired.
. In general, any of the sensor mappings may be
stage-dependent, if desired.
Many examples of sensors will now be given. These are provided to
illustrate the definitions and to provide building blocks that will be
used in later examples of I-spaces. Examples 11.1 to
11.6 all involve state sensor mappings.
Example 11..1 (Odd/Even Sensor)
Let
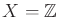
, the set of integers, and let
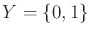
. The sensor
mapping is
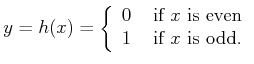 |
(11.2) |
The limitation of this sensor is that it only tells whether
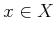
is odd or even. When combined with other information, this might be
enough to infer the state, but in general it provides incomplete
information.

Example 11..2 (Mod Sensor)
Example
11.1 can be easily generalized to yield the
remainder when
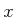
is divided by
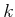
for some fixed integer
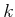
. Let
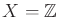
, and let
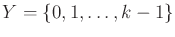
. The sensor mapping is
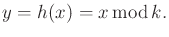 |
(11.3) |

Example 11..3 (Sign Sensor)
Let
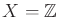
, and let
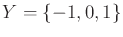
. The sensor mapping is
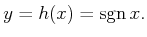 |
(11.4) |
This sensor provides very limited information because it only
indicates on which side of the boundary
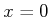
the state may lie. It
can, however, precisely determine whether
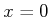
.

Example 11..4 (Selective Sensor)
Let
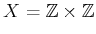
, and let
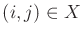
denote a state in which
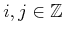
. Suppose that only the first component of
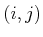
can be
observed. This yields the sensor mapping
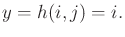 |
(11.5) |
An obvious generalization can be made for any state space that is
formed from Cartesian products. The sensor may reveal the values of
one or more components, and the rest remain hidden.

Example 11..5 (Bijective Sensor)
Let

be any state space, and let
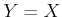
. Let the sensor mapping
be any bijective function
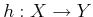
. This sensor provides
information that is equivalent to knowing the state. Since
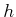
is
bijective, it can be inverted to obtain
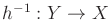
.
For any
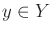
, the state can be determined as
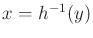
.
A special case of the bijective sensor is the identity
sensor, for which 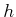 is the identity function. This was essentially
assumed to exist for all planning problems covered before this chapter
because it immediately yields the state. However, any bijective
sensor could serve the same purpose.
is the identity function. This was essentially
assumed to exist for all planning problems covered before this chapter
because it immediately yields the state. However, any bijective
sensor could serve the same purpose.

Example 11..6 (Null Sensor)
Let

be any state space, and let
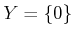
. The
null
sensor is obtained by defining the sensor mapping as
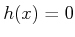
. The
sensor reading remains fixed and hence provides no information
regarding the state.

From the examples so far, it is tempting to think about partitioning
 based on sensor observations. Suppose that in general a state
mapping,
based on sensor observations. Suppose that in general a state
mapping, 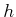 , is not bijective, and let
, is not bijective, and let 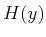 denote the following
subset of
denote the following
subset of  :
:
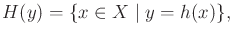 |
(11.6) |
which is the preimage of 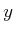 .
The set of preimages, one for each
.
The set of preimages, one for each 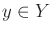 , forms a partition of
, forms a partition of  .
In some sense, this indicates the ``resolution'' of the sensor. A
bijective sensor partitions
.
In some sense, this indicates the ``resolution'' of the sensor. A
bijective sensor partitions  into singleton sets because it
contains perfect information. At the other extreme, the null sensor
partitions
into singleton sets because it
contains perfect information. At the other extreme, the null sensor
partitions  into a single set,
into a single set,  itself. The sign sensor appears
slightly more useful because it partitions
itself. The sign sensor appears
slightly more useful because it partitions  into three sets:
into three sets:
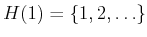 ,
,
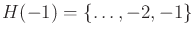 , and
, and
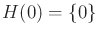 .
The preimages of the selective sensor are particularly interesting.
For each
.
The preimages of the selective sensor are particularly interesting.
For each
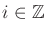 ,
,
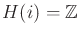 . The partitions induced by the
preimages may remind those with an algebra background of the
construction of quotient groups via homomorphisms [769].
. The partitions induced by the
preimages may remind those with an algebra background of the
construction of quotient groups via homomorphisms [769].
Next consider some examples that involve a state-action sensor
mapping. There are two different possibilities regarding the model
for the nature sensing action:
- Nondeterministic: In this case, there is no additional
information regarding which
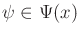 will be chosen.
will be chosen.
- Probabilistic: A probability distribution is known. In
this case, the probability,
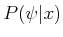 , that
, that 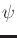 will be chosen
is known for each
will be chosen
is known for each
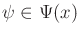 .
.
These two possibilities also appeared in Section 10.1.1,
for nature actions that interfere with the state transition equation.
It is sometimes useful to consider the state-action sensor model as a
probability distribution over 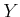 for a given state. Recall the
conversion from
for a given state. Recall the
conversion from
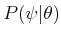 to
to
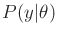 in
(9.28). By replacing
in
(9.28). By replacing 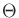 by
by  , the same idea can
be applied here. Assume that if the domain of
, the same idea can
be applied here. Assume that if the domain of 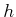 is restricted to
some
is restricted to
some 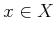 , it forms an injective (one-to-one) mapping from
, it forms an injective (one-to-one) mapping from 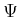 to
to 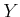 . In this case,
. In this case,
 |
(11.7) |
If the injective assumption is lifted, then 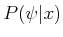 is replaced by a
sum over all
is replaced by a
sum over all 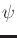 for which
for which
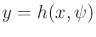 .
.
Example 11..7 (Sensor Disturbance)
Let
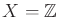
,
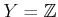
, and
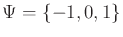
. The idea is to
construct a sensor that would be the identity sensor if it were not
for the interference of nature. The sensor mapping is
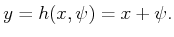 |
(11.8) |
It is always known that
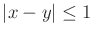
. Therefore, if
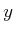
is
received as a sensor reading, one of the following must be true:
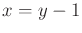
,
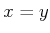
, or
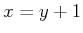
.

Example 11..8 (Disturbed Sign Sensor)
Let
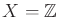
,
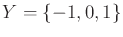
, and
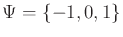
. Let the
sensor mapping be
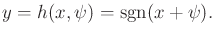 |
(11.9) |
In this case, if
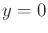
, it is no longer known for certain whether
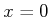
. It is possible that
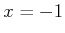
or
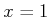
. If
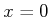
, then it is
possible for the sensor to read
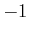
,
0, or
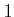
.

Example 11..9 (Disturbed Odd/Even Sensor)
It is not hard to construct examples for which some mild interference
from nature destroys all of the information. Let
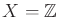
,
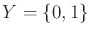
, and
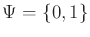
. Let the sensor mapping be
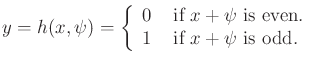 |
(11.10) |
Under the nondeterministic model for the nature sensing action
,
the sensor provides no useful information regarding the state.
Regardless of the observation, it is never known whether
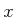
is even
or odd. Under a probabilistic model, however, this sensor may provide
some useful information.

It is once again informative to consider preimages. For a
state-action sensor mapping, the preimage is
In comparison to state sensor mappings, the preimage sets are larger
for state-action sensor mappings. Also, they do not generally form a
partition of  . For example, the preimages of Example
11.8 are
. For example, the preimages of Example
11.8 are
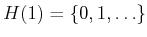 ,
,
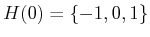 , and
, and
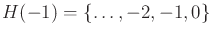 . This is not a
partition because every preimage contains 0. If desired,
. This is not a
partition because every preimage contains 0. If desired, 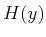 can
be directly defined for each
can
be directly defined for each 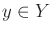 , instead of explicitly defining
nature sensing actions.
, instead of explicitly defining
nature sensing actions.
Finally, one example of a history-based sensor mapping is given.
Example 11..10 (Delayed-Observation Sensor)
Let
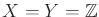
. A
delayed-observation sensor can be defined
for some fixed positive integer
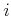
as
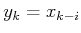
. It indicates
what the state was
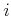
stages ago. In this case, it gives a perfect
measurement of the old state value. Many other variants are possible.
For example, it might only give the sign of the state from
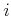
stages ago.

Steven M LaValle
2020-08-14

![]() , is finite or countably infinite, as in Formulations 2.1
and 2.3. A sensor is defined in terms of two
components: 1) an observation space, which is the set of
possible readings for the sensor, and 2) a sensor mapping, which
characterizes the readings that can be expected if the current state
or other information is given. Be aware that in the planning model,
the state is not really given; it is only assumed to be given when
modeling a sensor. The sensing model given here generalizes the one
given in Section 9.2.3. In that case, the sensor provided
information regarding
, is finite or countably infinite, as in Formulations 2.1
and 2.3. A sensor is defined in terms of two
components: 1) an observation space, which is the set of
possible readings for the sensor, and 2) a sensor mapping, which
characterizes the readings that can be expected if the current state
or other information is given. Be aware that in the planning model,
the state is not really given; it is only assumed to be given when
modeling a sensor. The sensing model given here generalizes the one
given in Section 9.2.3. In that case, the sensor provided
information regarding ![]() instead of
instead of ![]() because state spaces
were not needed in Chapter 9.
because state spaces
were not needed in Chapter 9.
![]() denote an observation space, which is a finite or
countably infinite set. Let
denote an observation space, which is a finite or
countably infinite set. Let ![]() denote the sensor mapping.
Three different kinds of sensor mappings will be considered, each of
which is more complicated and general than the previous one:
denote the sensor mapping.
Three different kinds of sensor mappings will be considered, each of
which is more complicated and general than the previous one:
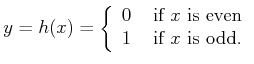
![]() is the identity function. This was essentially
assumed to exist for all planning problems covered before this chapter
because it immediately yields the state. However, any bijective
sensor could serve the same purpose.
is the identity function. This was essentially
assumed to exist for all planning problems covered before this chapter
because it immediately yields the state. However, any bijective
sensor could serve the same purpose.
![]()
![]() based on sensor observations. Suppose that in general a state
mapping,
based on sensor observations. Suppose that in general a state
mapping, ![]() , is not bijective, and let
, is not bijective, and let ![]() denote the following
subset of
denote the following
subset of ![]() :
:
![]() for a given state. Recall the
conversion from
for a given state. Recall the
conversion from
![]() to
to
![]() in
(9.28). By replacing
in
(9.28). By replacing ![]() by
by ![]() , the same idea can
be applied here. Assume that if the domain of
, the same idea can
be applied here. Assume that if the domain of ![]() is restricted to
some
is restricted to
some ![]() , it forms an injective (one-to-one) mapping from
, it forms an injective (one-to-one) mapping from ![]() to
to ![]() . In this case,
. In this case,