Critical changes in cells

Now we are prepared to explain the cell decomposition in more detail. Imagine traveling along a path in ${\mathbb{R}}^2$ and producing an animated version of the radar map in Figure 6.22b. We say that a critical change occurs each time the circular ordering representation of (6.6) changes. Changes occur when intervals: 1) appear, 2) disappear, 3) split apart, 4) merge into one, or 5) when the feature of an interval changes. The first task is to partition ${\mathbb{R}}^2$ into maximal $2$-cells over which no critical changes occur. Each one of these $2$-cells, $R$, represents the projection of a strip of $3$-cells in ${\cal C}_{free}$. Each $3$-cell is defined as follows. Let $\{R,[f_i,f_{i+1}]\}$ denote the 3D region in ${\cal C}_{free}$ for which $(x,y) \in R$ and $\theta$ places the segment between contacts $f_i$ and $f_{i+1}$. The cylinder of cells above $R$ is given by $\{R,[f_i,f_{i+1}]\}$ for each interval in the circular ordering representation, (6.6). If any orientation is possible because ${\cal A}$ never contacts an obstacle while in $R$, then we write $\{R\}$.

What are the positions in ${\mathbb{R}}^2$ that cause critical changes to occur? It turns out that there are five different cases to consider, each of which produces a set of critical curves in ${\mathbb{R}}^2$. When one of these curves is crossed, a critical change occurs. If none of these curves is crossed, then no critical change can occur. Therefore, these curves precisely define the boundaries of the desired $2$-cells in ${\mathbb{R}}^2$. Let $L$ denote the length of the robot (which is the line segment).

Figure 6.24: Four of the five cases that produce critical curves in ${\mathbb{R}}^2$.

Figure 6.25: The fifth case is the most complicated. It results in a fourth-degree algebraic curve called the Conchoid of Nicomedes.

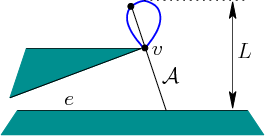Consider how the five cases mentioned above may occur. Two of the five cases have already been observed in Figures 6.22 and 6.23. These appear in Figures 6.24a and Figures 6.24b, and occur if $(x,y)$ is within $L$ of an edge or a vertex. The third and fourth cases are shown in Figures 6.24c and 6.24d, respectively. The third case occurs because crossing the curve causes ${\cal A}$ to change between being able to touch $e$ and being able to touch $v$. This must be extended from any edge at an endpoint that is a reflex vertex (interior angle is greater than $\pi$). The fourth case is actually a return of the bitangent case from Figure 6.10, which arose for the shortest path graph. If the vertices are within $L$ of each other, then a linear critical curve is generated because ${\cal A}$ is no longer able to touch $v_2$ when crossing it from right to left. Bitangents always produce curves in pairs; the curve above $v_2$ is not shown. The final case, shown in Figure 6.25, is the most complicated. It is a fourth-degree algebraic curve called the Conchoid of Nicomedes, which arises from ${\cal A}$ being in simultaneous contact between $v$ and $e$. Inside of the teardrop-shaped curve, ${\cal A}$ can contact $e$ but not $v$. Just outside of the curve, it can touch $v$. If the $xy$ coordinate frame is placed so that $v$ is at $(0,0)$, then the equation of the curve is

$$(x^2-y^2)(y+d)^2-y^2 L^2 = 0,$$ (6.7)

in which $d$ is the distance from $v$ to $e$.

Figure 6.26: The critical curves form the boundaries of the noncritical regions in ${\mathbb{R}}^2$.

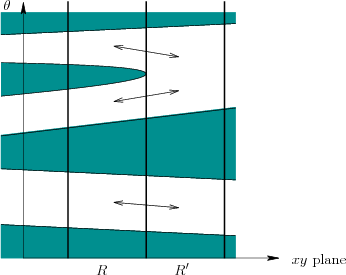
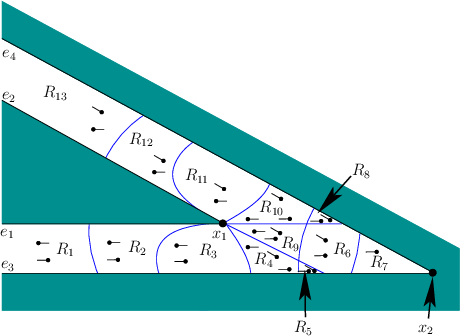
Putting all of the curves together generates a cell decomposition of ${\mathbb{R}}^2$. There are noncritical regions, over which there is no change in (6.6); these form the $2$-cells. The boundaries between adjacent $2$-cells are sections of the critical curves and form $1$-cells. There are also 0-cells at places where critical curves intersect. Figure 6.26 shows an example adapted from [588]. Note that critical curves are not drawn if their corresponding configurations are all in ${\cal C}_{obs}$. The method still works correctly if they are included, but unnecessary cell boundaries are made. Just for fun, they could be used to form a nice cell decomposition of ${\cal C}_{obs}$, in addition to ${\cal C}_{free}$. Since ${\cal C}_{obs}$ is avoided, is seems best to avoid wasting time on decomposing it. These unnecessary cases can be detected by imagining that ${\cal A}$ is a laser with range $L$. As the laser sweeps around, only features that are contacted by the laser are relevant. Any features that are hidden from view of the laser correspond to unnecessary boundaries.

Figure 6.27: Connections are made between neighboring $3$-cells that lie above neighboring noncritical regions.

After the cell decomposition has been constructed in ${\mathbb{R}}^2$, it needs to be lifted into ${\mathbb{R}}^2 \times [0,2 \pi] {/\sim}$. This generates a cylinder of $3$-cells above each 2D noncritical region, $R$. The roadmap could easily be defined to have a vertex for every $3$-cell and $2$-cell, which would be consistent with previous cell decompositions; however, vertices at $2$-cells are not generated here to make the coming example easier to understand. Each $3$-cell, $\{R,[f_i,f_{i+1}]\}$, corresponds to the vertex in a roadmap. The roadmap edges connect neighboring $3$-cells that have a $2$-cell as part of their common boundary. This means that in ${\mathbb{R}}^2$ they share a one-dimensional portion of a critical curve.

Figure 6.28: A depiction of the $3$-cells above the noncritical regions. Sample rod orientations are shown for each cell (however, the rod length is shortened for clarity). Edges between cells are shown in Figure 6.29.