Translation and rotation in one matrix

It would be convenient to apply both rotation and translation together in a single operation. Suppose we want to apply a rotation matrix $R$, and follow it with a translation by $(x_t,y_t,z_t)$. Algebraically, this is

$$\begin{bmatrix}x' y' z' \end{bmatrix} = R \begin{bmatrix}x y z \end{bmatrix} + \begin{bmatrix}x_t y_t z_t \end{bmatrix} .$$ (3.20)

Although there is no way to form a single 3 by 3 matrix to accomplish both operations, it can be done by increasing the matrix dimensions by one. Consider the following 4 by 4 homogeneous transformation matrix:

$$T_{rb} = \left[ \begin{array}{ccc\vert c} & & & x_t & R & & y_t & & & z_t \midrule 0 & 0 & 0 & 1 \end{array} \right] ,$$ (3.21)

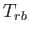in which $R$ fills the upper left three rows and columns. The notation $T_{rb}$ is used to denote that the matrix is a rigid body transform, meaning that it does not distort objects. A homogeneous transform matrix could include other kinds of transforms, which will appear in Section 3.5.

The same result as in (3.20) can be obtained by performing multiplication with (3.23) as follows:

$$\left[ \begin{array}{ccc\vert c} & & & x_t & R & & y_t & & & ... ... y z 1 \end{bmatrix} = \begin{bmatrix}x' y' z' 1 \end{bmatrix} .$$ (3.22)

Because of the extra dimension, we extended the point $(x,y,z)$ by one dimension, to obtain $(x,y,z,1)$. Note that (3.23) represents rotation followed by translation, not the other way around. Translation and rotation do not commute; therefore, this is an important point.