Yaw, pitch, and roll

Figure 3.7: Any three-dimensional rotation can be described as a sequence of yaw, pitch, and roll rotations.

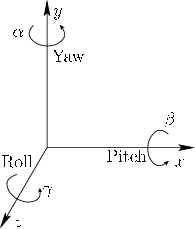One of the simplest ways to parameterize 3D rotations is to construct them from ``2D-like'' transformations, as shown in Figure 3.7. First consider a rotation about the $z$-axis. Let roll be a counterclockwise rotation of $\gamma$ about the $z$-axis. The rotation matrix is given by

$$R_z(\gamma) = \begin{bmatrix}\cos\gamma & -\sin\gamma & 0 \sin\gamma & \cos\gamma & 0 0 & 0 & 1 \end{bmatrix} .$$ (3.16)

The upper left of the matrix looks exactly like the 2D rotation matrix (3.13), except that $\theta$ is replaced by $\gamma$. This causes yaw to behave exactly like 2D rotation in the $xy$ plane. The remainder of $R_z(\gamma)$ looks like the identity matrix, which causes $z$ to remain unchanged after a roll.

Similarly, let pitch be a counterclockwise rotation of $\beta$ about the $x$-axis:

$$R_x(\beta) = \begin{bmatrix}1 & 0 & 0 0 & \cos\beta & -\sin\beta 0 & \sin\beta & \cos\beta \end{bmatrix} .$$ (3.17)

In this case, points are rotated with respect to $y$ and $z$ while the $x$ coordinate is left unchanged.

Finally, let yaw be a counterclockwise rotation of $\alpha$ about the $y$-axis:

$$R_y(\alpha) = \begin{bmatrix}\cos\alpha & 0 & \sin\alpha 0 & 1 & 0 -\sin\alpha & 0 & \cos\alpha \end{bmatrix} .$$ (3.18)

In this case, rotation occurs with respect to $x$ and $z$ while leaving $y$ unchanged.