Equilibrium points and Lyapunov stability

At the very least, it seems that the state should remain fixed at ${x_{G}}$, if it is reached. A point ${x_{G}}\in X$ is called an equilibrium point (or fixed point) of the vector field $f$ if and only if $f({x_{G}}) = 0$. This does not, however, characterize how trajectories behave in the vicinity of ${x_{G}}$. Let ${x_{I}}\in X$ denote some initial state, and let $x(t)$ refer to the state obtained at time $t$ after integrating the vector field $f$ from ${x_{I}}= x(0)$.

Figure 15.1: Lyapunov stability: (a) Choose any open set $O_1$ that contains ${x_{G}}$, and (b) there exists some open set $O_2$ from which trajectories will not be able to escape $O_1$. Note that convergence to ${x_{G}}$ is not required.

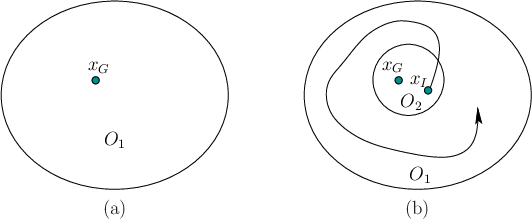See Figure 15.1. An equilibrium point ${x_{G}}\in X$ is called Lyapunov stable if for any open neighborhood^15.1 $O_1$ of ${x_{G}}$ there exists another open neighborhood $O_2$ of ${x_{G}}$ such that ${x_{I}}\in O_2$ implies that $x(t) \in O_1$ for all $t > 0$. If $X = {\mathbb{R}}^n$, then some intuition can be obtained by using an equivalent definition that is expressed in terms of the Euclidean metric. An equilibrium point ${x_{G}}\in {\mathbb{R}}^n$ is called Lyapunov stable if, for any $t > 0$, there exists some $\delta > 0$ such that $\Vert{x_{I}}-{x_{G}}\Vert < \delta$ implies that $\Vert x(t) - {x_{G}}\Vert < \epsilon$. This means that we can choose a ball around ${x_{G}}$ with a radius as small as desired, and all future states will be trapped within this ball, as long as they start within a potentially smaller ball of radius $\delta$. If a single $\delta$ can be chosen independently of every $\epsilon$ and $x$, then the equilibrium point is called uniform Lyapunov stable.