Suppose that a system is given in the form
 |
(14.31) |
in which there are  action variables
action variables
 . It
may be helpful to glance ahead to Example 14.6, which will
illustrate the coming concepts for the simple case of double
integrators
. It
may be helpful to glance ahead to Example 14.6, which will
illustrate the coming concepts for the simple case of double
integrators
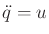 . The acceleration in
. The acceleration in  is determined
from the state
is determined
from the state
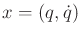 and action
and action 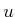 . Assume
. Assume 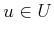 , in
which
, in
which 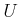 is an
is an  -dimensional subset of
-dimensional subset of
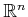 . If
. If 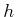 is
nonsingular at
is
nonsingular at 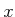 , then an
, then an  -dimensional set of possible
accelerations arises from choices of
-dimensional set of possible
accelerations arises from choices of 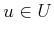 . This means it is
fully actuated. If there were fewer than
. This means it is
fully actuated. If there were fewer than  action variables, then
there would generally not be enough freedom to follow a specified
path. Therefore,
action variables, then
there would generally not be enough freedom to follow a specified
path. Therefore, 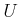 must be
must be  -dimensional. Which choices of
-dimensional. Which choices of 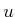 ,
however, constrain the motion to follow the given path
,
however, constrain the motion to follow the given path 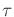 ? To
determine this, the
? To
determine this, the 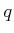 ,
, 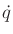 , and
, and 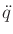 variables need to be
related to the path domain
variables need to be
related to the path domain 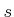 and its first and second time
derivatives
and its first and second time
derivatives 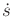 and
and 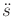 , respectively. This leads to a
subset of
, respectively. This leads to a
subset of 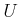 that corresponds to actions that follow the path.
that corresponds to actions that follow the path.
Suppose that 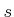 ,
, 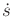 ,
, 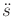 , and a path
, and a path 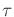 are given.
The configuration
are given.
The configuration
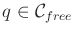 is
is
 |
(14.32) |
Assume that all first and second derivatives of 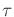 exist. The
velocity
exist. The
velocity 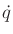 can be determined by the chain rule as
can be determined by the chain rule as
 |
(14.33) |
in which the derivative  is evaluated at
is evaluated at 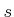 . The
acceleration is obtained by taking another derivative, which yields
. The
acceleration is obtained by taking another derivative, which yields
 |
(14.34) |
by application of the product rule. The full state
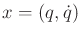 can be recovered from
can be recovered from
 using (14.32) and
(14.33).
using (14.32) and
(14.33).
The next step is to obtain an equation that looks similar to
(14.31), but is expressed in terms of 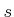 ,
, 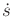 ,
and
,
and 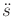 . A function
. A function
 can be obtained from
can be obtained from
 by substituting
by substituting  for
for 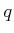 and the right side
of (14.33) for
and the right side
of (14.33) for 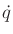 :
:
 |
(14.35) |
This yields
 |
(14.36) |
For a given state 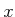 (which can be obtained from
(which can be obtained from 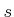 and
and 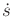 ),
the set of accelerations that can be obtained by a choice of
),
the set of accelerations that can be obtained by a choice of 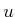 in
(14.36) is the same as that for the original system
in (14.31). The only difference is that
in
(14.36) is the same as that for the original system
in (14.31). The only difference is that 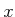 is now
constrained to a 2D subset of
is now
constrained to a 2D subset of  , which are the states that can be
reached by selecting values for
, which are the states that can be
reached by selecting values for 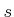 and
and 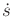 .
.
Applying (14.34) to the left side of
(14.36) constrains the accelerations to cause motions
that follow 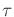 . This yields
. This yields
 |
(14.37) |
which can also be expressed as
 |
(14.38) |
by moving the first term of (14.34) to the right. Note
that  equations are actually represented in
(14.38). For each
equations are actually represented in
(14.38). For each 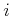 in which
in which
 , a constraint of the form
, a constraint of the form
 |
(14.39) |
is obtained by solving for 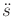 .
.
Steven M LaValle
2020-08-14

![]() ,
, ![]() ,
, ![]() , and a path
, and a path ![]() are given.
The configuration
are given.
The configuration
![]() is
is
![]() ,
, ![]() ,
and
,
and ![]() . A function
. A function
![]() can be obtained from
can be obtained from
![]() by substituting
by substituting ![]() for
for ![]() and the right side
of (14.33) for
and the right side
of (14.33) for ![]() :
:

![]() . This yields
. This yields