
Next: 14.3 Sampling-Based Motion Planning Up: 14.2 Reachability and Completeness Previous: 14.2.2.3 Resolution completeness for
The discrete-time model of Section 14.2.2 is just one of many possible ways to discretize the space of action trajectories. It will now be considered as a special case of specifying motion primitives. The restriction to constant actions over fixed time intervals may be too restrictive in many applications. Suppose we want to automate the motions of a digital actor for use in a video game or film. Imagine having a database of interesting motion primitives. Such primitives could be extracted, for example, from motion capture data [35,553]. For example, if the actor is designed for kung-fu fighting, then each motion sequence may correspond to a basic move, such a kick or punch. It is unlikely that such motion primitives correspond to constant actions over a fixed time interval. The durations of the motion primitives will usually vary.
Such models can generally be handled by defining a more general kind of discretization. The discrete-time model can be used to formulate a discrete-time state transition equation of the form
Now generalize the preceding construction to allow more general motion
primitives. Let
![]() denote a motion primitive, which is a
function from an interval of time into
denote a motion primitive, which is a
function from an interval of time into ![]() . Let the interval of time
start at 0 and stop at
. Let the interval of time
start at 0 and stop at
![]() , which is a final time that
depends on the particular primitive. From any state
, which is a final time that
depends on the particular primitive. From any state
![]() ,
suppose that a set
,
suppose that a set
![]() of motion primitives is available. The
set may even be infinite, in which case some additional sampling must
eventually be performed over the space of motion primitives by a local
planning method. A state transition equation that operates over
discrete stages can be defined as
of motion primitives is available. The
set may even be infinite, in which case some additional sampling must
eventually be performed over the space of motion primitives by a local
planning method. A state transition equation that operates over
discrete stages can be defined as
 |
For some motion primitives, it may not be possible to immediately
sequence them without applying transitional motions. For
example, in [362], two different kinds of motion
primitives, called trim trajectories and
maneuvers, are defined for autonomous
helicopter flight. The trim trajectories correspond to steady
motions, and maneuvers correspond to unsteady motions that are needed
to make transitions between steady motions. Transitions from one trim
trajectory to another are only permitted through the execution of a
maneuver. The problem can be nicely modeled as a hybrid system in
which each motion primitive represents a mode [360] (recall
hybrid system concepts from Sections 7.3,
8.3.1, and 10.6). The augmented state space is
![]() , in which
, in which ![]() is a set of modes. The transition equation
(14.13) can be extended over the augmented state space so
that motion primitives can change modes in addition to changing
the original state. The possible trajectories for the helicopter
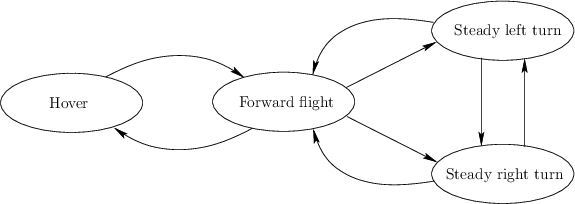
follow paths in a graph called the maneuver automaton. An
example from [360] is shown in Figure 14.8. Every
edge and every vertex corresponds to a mode in the maneuver automaton.
Each edge or vertex actually corresponds to a parameterized family of
primitives, from which a particular one is chosen based on the state.
A similar state machine is proposed in [452] for animating
humans, and the motion primitives are called behaviors.
is a set of modes. The transition equation
(14.13) can be extended over the augmented state space so
that motion primitives can change modes in addition to changing
the original state. The possible trajectories for the helicopter
follow paths in a graph called the maneuver automaton. An
example from [360] is shown in Figure 14.8. Every
edge and every vertex corresponds to a mode in the maneuver automaton.
Each edge or vertex actually corresponds to a parameterized family of
primitives, from which a particular one is chosen based on the state.
A similar state machine is proposed in [452] for animating
humans, and the motion primitives are called behaviors.
Discretizations based on general motion primitives offer great flexibility, and in many cases dramatic performance improvements can be obtained in a sampling-based planning algorithm. The main drawback is that the burden of establishing resolution completeness is increased.
Steven M LaValle 2020-08-14