
Next: Completing the state transition Up: 13.3.3 Motion of a Previous: Inertia matrix
Now the inertia matrix will be considered more carefully. It is a
symmetric
![]() matrix, which can be expressed as
matrix, which can be expressed as
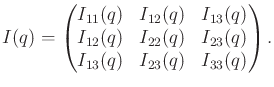 |
(13.93) |
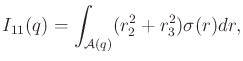 |
(13.94) |
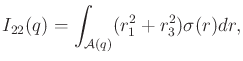 |
(13.95) |
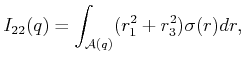 |
(13.96) |
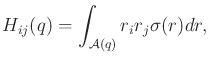 |
(13.97) |
One problem with the formulation so far is that the inertia matrix
changes as the body rotates because all entries depend on the
orientation ![]() . Recall that it was derived by considering
. Recall that it was derived by considering ![]() as a
collection of infinitesimal particles in the translating frame. It is
possible, however, to express the inertia matrix in the body frame of
as a
collection of infinitesimal particles in the translating frame. It is
possible, however, to express the inertia matrix in the body frame of
![]() . In this case, the inertia matrix can be denoted as
. In this case, the inertia matrix can be denoted as ![]() because
it does not depend on the orientation of
because
it does not depend on the orientation of ![]() with respect to the
translational frame. The original inertia matrix is then recovered by
applying a rotation that relates the body frame to the
translational frame:
with respect to the
translational frame. The original inertia matrix is then recovered by
applying a rotation that relates the body frame to the
translational frame:
![]() , in which
, in which ![]() is a rotation matrix.
It can be shown (see Equation (2.91) and Section 3.2 of [994])
that after performing this substitution, (13.92)
simplifies to
is a rotation matrix.
It can be shown (see Equation (2.91) and Section 3.2 of [994])
that after performing this substitution, (13.92)
simplifies to
The body frame of ![]() must have its origin at the center of
mass
must have its origin at the center of
mass ![]() ; however, its orientation has not been constrained. For
different orientations, different inertia matrices will be obtained.
Since
; however, its orientation has not been constrained. For
different orientations, different inertia matrices will be obtained.
Since ![]() captures the physical characteristics of
captures the physical characteristics of ![]() , any two
inertia matrices differ only by a rotation. This means for a given
, any two
inertia matrices differ only by a rotation. This means for a given
![]() , all inertia matrices that can be defined by different body frame
orientations have the same eigenvalues and eigenvectors. Consider the
positive definite quadratic form
, all inertia matrices that can be defined by different body frame
orientations have the same eigenvalues and eigenvectors. Consider the
positive definite quadratic form
![]() , which represents the
equation of an ellipsoid. A standard technique in linear algebra is
to compute the principle axes of an ellipsoid, which turn out to be
the eigenvectors of
, which represents the
equation of an ellipsoid. A standard technique in linear algebra is
to compute the principle axes of an ellipsoid, which turn out to be
the eigenvectors of ![]() . The lengths of the ellipsoid axes are given
by the eigenvalues. An axis-aligned expression of the ellipsoid can
be obtained by defining
. The lengths of the ellipsoid axes are given
by the eigenvalues. An axis-aligned expression of the ellipsoid can
be obtained by defining ![]() , in which
, in which ![]() is the matrix formed
by columns of eigenvectors. Therefore, there exists an orientation of
the body frame in which the inertia matrix simplifies to
is the matrix formed
by columns of eigenvectors. Therefore, there exists an orientation of
the body frame in which the inertia matrix simplifies to
Steven M LaValle 2020-08-14