The state transition equation involves 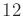 scalar equations. Six of
these are straightforward to obtain by characterizing the linear
velocity. For this case, it can be imagined that the body does not
rotate with respect to the inertial frame. The linear momentum is
scalar equations. Six of
these are straightforward to obtain by characterizing the linear
velocity. For this case, it can be imagined that the body does not
rotate with respect to the inertial frame. The linear momentum is
 , and
Newton's second law implies that
, and
Newton's second law implies that
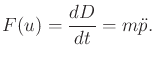 |
(13.81) |
This immediately yields half of the state transition equation by
solving for  . This yields a 3D version of the double
integrator in Example 13.3, scaled by
. This yields a 3D version of the double
integrator in Example 13.3, scaled by 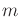 . Let
. Let
 denote the coordinates of
denote the coordinates of  . Let
. Let
 denote the linear velocity the center of mass. Three
scalar equations of the state transition equation are
denote the linear velocity the center of mass. Three
scalar equations of the state transition equation are
 for
for  . Three more are obtained as
. Three more are obtained as
 for
for  . If there are no moments and the body
is not rotating with respect to the inertial frame, then these six equations are sufficient to describe
its motion. This may occur for a spacecraft that is initially at
rest, and its thrusters apply a total force only through the
center of mass.
. If there are no moments and the body
is not rotating with respect to the inertial frame, then these six equations are sufficient to describe
its motion. This may occur for a spacecraft that is initially at
rest, and its thrusters apply a total force only through the
center of mass.
Steven M LaValle
2020-08-14

![]() scalar equations. Six of
these are straightforward to obtain by characterizing the linear
velocity. For this case, it can be imagined that the body does not
rotate with respect to the inertial frame. The linear momentum is
scalar equations. Six of
these are straightforward to obtain by characterizing the linear
velocity. For this case, it can be imagined that the body does not
rotate with respect to the inertial frame. The linear momentum is
![]() , and
Newton's second law implies that
, and
Newton's second law implies that