
Next: Further Reading Up: 2.5 Logic-Based Planning Methods Previous: Plan extraction
Another interesting approach is to convert the planning problem into an enormous Boolean satisfiability problem. This means that the planning problem of Formulation 2.4 can be solved by determining whether some assignment of variables is possible for a Boolean expression that leads to a TRUE value. Generic methods for determining satisfiability can be directly applied to the Boolean expression that encodes the planning problem. The Davis-Putnam procedure is one of the most widely known algorithms for satisfiability. It performs a depth-first search by iteratively trying assignments for variables and backtracking when assignments fail. During the search, large parts of the expression can be eliminated due to the current assignments. The algorithm is complete and reasonably efficient. Its use in solving planning problems is surveyed in [382]. In practice, stochastic local search methods provide a reasonable alternative to the Davis-Putnam procedure [459].
Suppose a planning problem has been given in terms of Formulation
2.4. All literals and operators will be tagged with a
stage index. For example, a literal that appears in two different
stages will be considered distinct. This kind of tagging is similar
to situation calculus [378]; however, in that case,
variables are allowed for the tags. To obtain a finite, Boolean
expression the total number of stages must be declared. Let ![]() denote the number of stages at which operators can be applied. As
usual, the fist stage is
denote the number of stages at which operators can be applied. As
usual, the fist stage is ![]() and the final stage is
and the final stage is
![]() .
Setting a stage limit is a significant drawback of the approach
because this is usually not known before the problem is solved. A
planning algorithm can assume a small value for
.
Setting a stage limit is a significant drawback of the approach
because this is usually not known before the problem is solved. A
planning algorithm can assume a small value for ![]() and then gradually
increase it each time the resulting Boolean expression is not
satisfied. If the problem is not solvable, however, this approach
iterates forever.
and then gradually
increase it each time the resulting Boolean expression is not
satisfied. If the problem is not solvable, however, this approach
iterates forever.
Let ![]() denote logical OR, and let
denote logical OR, and let ![]() denote logical AND.
The Boolean expression is written as a
conjunction2.5 of many
terms, which arise from five different sources:
denote logical AND.
The Boolean expression is written as a
conjunction2.5 of many
terms, which arise from five different sources:
| (2.33) |
| (2.34) |
| (2.35) |
The following example illustrates the construction.
The expression for the initial state is
| (2.36) |
| (2.37) |
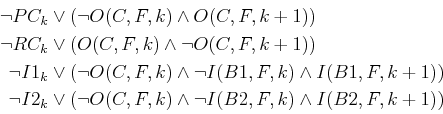 |
(2.38) |
The frame axioms yield the expressions
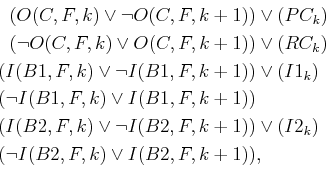 |
(2.39) |
Finally, the complete exclusion axiom yields the expressions
| (2.40) | ||||||
Steven M LaValle 2020-08-14