- For the environment in Figure
12.1a, give the nondeterministic I-states for the action
sequence
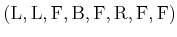 ,
if the initial state is the robot in position
,
if the initial state is the robot in position  facing north and the
initial I-state is
facing north and the
initial I-state is
 .
.
- Describe how to apply the algorithm from Figure
10.6 to design an information-feedback plan that takes a
map of a grid and performs localization.
Figure 12.54:
An environment for grid-based
localization.
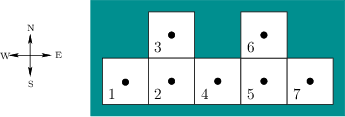 |
- Suppose that a robot operates in the environment shown in Figure
12.54 using the same motion and sensing model as in Example
12.1. Design an information-feedback plan that is as
simple as possible and successfully localizes the robot, regardless of
its initial state. Assume the initial condition
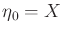 .
.
- Prove that the robot can use the
latitude and orientation information to detect the unique point of
each obstacle boundary in the maze searching algorithm of Section
12.3.1.
- Suppose once again that a robot is placed into one of the six
environments shown in Figure 12.12. It is initially in the
upper right cell facing north; however, the initial condition is
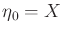 . Determine the sequence of sensor observations and
nondeterministic I-states as the robot executes the action sequence
. Determine the sequence of sensor observations and
nondeterministic I-states as the robot executes the action sequence
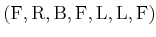 .
.
- Prove that the counter in the maze searching algorithm of
Section 12.3.1 can be replaced by two pebbles, and the robot
can still solve the problem by simulating the counter. The robot can
place either pebble on a tile, detect them when the robot is on the
same tile, and can pick them up to move them to other tiles.
- Continue the trajectory shown in Figure 12.23 until
the goal is reached using the Bug2 strategy.
- Show that the competitive ratio for the
doubling spiral motion applied to the lost-cow problem of Figure
12.26 is
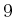 .
.
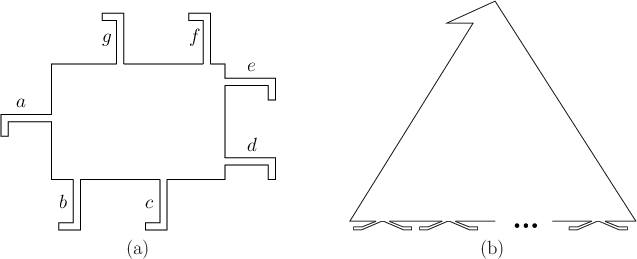
- Generalize the lost-cow problem so that there are
 fences
that emanate from the current cow location (
fences
that emanate from the current cow location (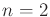 for the original
problem).
for the original
problem).
- If the cow is told that the gate is along only one unknown
fence and is no more than one unit away, what is the competitive ratio
of the best plan that you can think of?
- Suppose the cow does not know the maximum distance to the gate.
Propose a plan that solves the problem and establish its competitive
ratio.
Figure 12.55:
A path followed by the robot in an
initially unknown environment. The robot finishes in the lower
right.
 |
- Suppose a point robot is dropped into the environment shown in
Figure 12.42. Indicate the gap navigation trees that are
obtained as the robot moves along the path shown in Figure
12.55.
- Construct an example for which the worst case bound,
(12.25), for Bug1 is obtained.
Figure 12.56:
Two pursuit-evasion problems that
involve recontamination.
 |
- Some environments are so complicated that in
the pursuit-evasion problem they require the same region to be visited
multiple times. Find a solution for a single pursuer with
omnidirectional visibility to the problem in Figure 12.56a.
- Find a pursuit-evasion solution for a single
pursuer with omnidirectional visibility to the problem in Figure
12.56b, in which any number of pairs of ``feet'' may appear
on the bottom of the polygon.
- Prove that for a polygonal environment, if there are three
points,
 ,
,  , and
, and 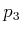 , for which
, for which 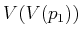 ,
, 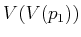 ,
and
,
and 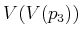 are pairwise-disjoint, then the problem requires more
than one pursuer.
are pairwise-disjoint, then the problem requires more
than one pursuer.
- Prove that the diameter function for the squeezing algorithm in
Section 12.5.2 has no more than
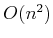 vertices. Give a
sequence of polygons that achieves this bound. What happens for a
regular polygon?
vertices. Give a
sequence of polygons that achieves this bound. What happens for a
regular polygon?
- Develop versions of (12.8) and (12.9)
for state-nature sensor mappings.
- Develop versions of (12.8) and (12.9)
for history-based sensor mappings.
- Describe in detail the I-map used for maze searching in Section
12.3.1. Indicate how this is an example of dramatically
reducing the size of the I-space, as described in Section
11.2. Is a sufficient I-map obtained?
- Describe in detail the I-map used in the Bug1 algorithm.
Is a sufficient I-map obtained?
- Suppose that several teams of point robots move around in a
simple polygon. Each robot has an omnidirectional visibility sensor
and would like to keep track of information for each shadow region.
For each team and shadow region, it would like to record one of three
possibilities: 1) There are definitely no team members in the region;
2) there may possibly be one or more; 3) there is definitely at least
one.
- Define a nondeterministic I-space based on labeling gaps that
captures the appropriate information. The I-space should be defined
with respect to one robot (each will have its own).
- Design an algorithm that keeps track of the nondeterministic
I-state as the robot moves through the environments and observes
others.
- Recall the sequence of connected corridors shown in Figure
12.40. Try to adapt the polygons so that the same number
of pursuers is needed, but there are fewer polygon edges. Try to use
as few edges as possible.
Implementations
- Solve the probabilistic passive localization problem of Section
12.2.3 for 2D grids. Implement your solution and
demonstrate it on several interesting examples.
- Implement the exact value-iteration method described in Section
12.1.3 to compute optimal cost-to-go functions. Test the
implementation on several small examples. How large can you make
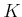 ,
,
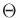 , and
, and 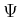 ?
?
- Develop and implement a graph search
algorithm that searches on
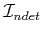 to perform robot localization on
a 2D grid. Test the algorithm on several interesting examples. Try
developing search heuristics that improve the performance.
to perform robot localization on
a 2D grid. Test the algorithm on several interesting examples. Try
developing search heuristics that improve the performance.
- Implement the Bug1, Bug2, and VisBug (with unlimited radius)
algorithms. Design a good set of examples for illustrating their
relative strengths and weaknesses.
- Implement software that computes probabilistic I-states for
localization as the robot moves in a grid.
- Implement the method of Section 12.3.4 for
simply connected environments and demonstrate it in simulation for
polygonal environments.
- Implement the pursuit-evasion algorithm for a single pursuer in
a simple polygon.
- Implement the part-squeezing algorithm presented in Section
12.5.2.
Steven M LaValle
2020-08-14
