12.4.3 Other Variations

Numerous variations of the pursuit-evasion problem presented in this section can be considered. The problem becomes much more difficult if there are multiple pursuers. A cell decomposition can be made based on changing shadow components; however, some of the cell boundaries are algebraic surfaces due to complicated interactions between the visibility polygons of different pursuers. Thus, it is difficult to implement a complete algorithm. On the other hand, straightforward heuristics can be used to guide multiple pursuers. A single pursuer can use the complete algorithm described in this section. When this pursuer fails, it can move to some part of the environment and then wait while a second pursuer applies the complete single-pursuer algorithm on each shadow component. This idea can be applied recursively for any number of robots.

The problem can be made more complicated by placing a velocity bound on the evader. Even though this makes the pursuer more powerful, it is more difficult to design a complete algorithm that correctly exploits this additional information. No complete algorithms currently exist for this case.

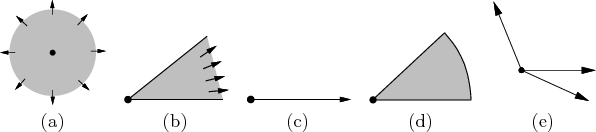
Figure 12.43 shows several alternative detection models that yield different definitions of $V(p(t))$. Each requires different pursuit-evasion algorithms because the structure of the I-space varies dramatically across different sensing models. For example, using the model in Figure 12.43c, a single pursuer is required to move along the $\partial X$. Once it moves into the interior, the shadow region always becomes a single connected component. This model is sometimes referred to as a flashlight. If there are two flashlights, then one flashlight may move into the interior while the other protects previous work. The case of limited depth, as shown in Figure 12.43, is very realistic in practice, but unfortunately it is the most challenging. The number of required pursuers generally depends on metric properties of the environment, such as its minimum ``thickness.'' The method presented in this section was extended to the case of a limited field of view in [381]; critical curves are obtained that are similar to those in Section 6.3.4. See the literature overview at the end of the chapter for more related material.

Figure 12.43: Several evader detection models: (a) omnidirectional sensing with unlimited distance; (b) visibility with a limited field of view; (c) a single visibility ray that is capable of rotating; (d) limited distance and a rotating viewing cone, which corresponds closely to a camera model; and (e) three visibility rays that are capable of rotating.