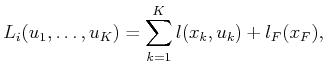- Suppose that a single-stage two-objective decision-making
problem is defined in which there are two objectives and a continuous
set of actions,
![$ U = [-10,10]$](img3846.gif) . The cost vector is
. The cost vector is
![$ L = [ u^2 \;\; u
- 1]$](img3847.gif) . Determine the set of Pareto-optimal actions.
. Determine the set of Pareto-optimal actions.
- Let
define the cost for each combination of choices by the decision maker
and nature. Let nature's randomized strategy be
![$ [1/5 \;\;\; 2/5
\;\;\; 1/10 \;\;\; 3/10]$](img3848.gif) .
.
- Use nondeterministic reasoning to find the
minimax decision and worst-case cost.
- Use probabilistic reasoning
to find the best expected-case decision and expected cost.
- Many reasonable decision rules are possible, other than those
considered in this chapter.
- Exercise 2(a) reflects extreme pessimism.
Suppose instead that extreme optimism is used. Select the choice that
optimizes the best-case cost for the matrix in Exercise
2.
- One approach is to develop a coefficient of optimism,
![$ \alpha \in [0,1]$](img3297.gif) , which allows one to interpolate between the two extreme
scenarios. Thus, a decision,
, which allows one to interpolate between the two extreme
scenarios. Thus, a decision, 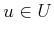 , is chosen by minimizing
, is chosen by minimizing
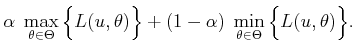 |
(9.94) |
Determine the optimal decision for this scenario under all possible
choices for
![$ \alpha \in [0,1]$](img3297.gif) . Give your answer as a list of
choices, each with a specified range of
. Give your answer as a list of
choices, each with a specified range of 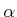 .
.
- Suppose that after making a decision, you observe the choice
made by nature. How does the cost that you received compare with the
best cost that could have been obtained if you chose something else,
given this choice by nature? This difference in costs can be
considered as regret or minimum ``Doh!''9.11 Psychologists have argued that some
people make choices based on minimizing regret. It reflects how badly
you wish you had done something else after making the decision.
- Develop an expression for the worst-case regret, and use it to
make a minimax regret decision using the matrix from Exercise
2.
- Develop an expression for the expected regret, and use it to
make a minimum expected regret decision.
- Using the matrix from Exercise 2, consider the
set of all probability distributions for nature. Characterize the set
of all distributions for which the minimax decision and the best
expected decision results in the same choice. This indicates how to
provide reverse justification for priors.
- Consider a Bayesian decision-theory scenario with cost function
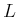 . Show that the decision rule never changes if
. Show that the decision rule never changes if
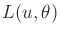 is
replaced by
is
replaced by
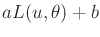 , for any
, for any 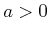 and
and
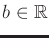 .
.
- Suppose that there are two classes,
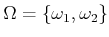 , with
, with
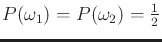 . The observation space,
. The observation space, 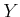 , is
, is
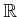 . Recall from
probability theory that the normal (or Gaussian) probability density
function is
. Recall from
probability theory that the normal (or Gaussian) probability density
function is
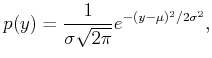 |
(9.95) |
in which 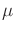 denotes the mean and
denotes the mean and 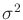 denotes the variance.
Suppose that
denotes the variance.
Suppose that
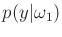 is a normal density in which
is a normal density in which 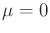 and
and
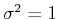 . Suppose that
. Suppose that
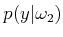 is a normal density
in which
is a normal density
in which 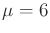 and
and
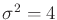 . Find the optimal
classification rule,
. Find the optimal
classification rule,
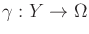 . You are welcome
to solve the problem numerically (by computer) or graphically (by
careful function plotting). Carefully explain how you arrived at
the answer in any case.
. You are welcome
to solve the problem numerically (by computer) or graphically (by
careful function plotting). Carefully explain how you arrived at
the answer in any case.
- Let
give the cost for each combination of choices by the decision maker
and nature. Let nature's randomized strategy be
![$ [1/4 \;\;
1/2 \;\; 1/8 \;\; 1/8]$](img3865.gif) .
.
- Use nondeterministic reasoning to find the
minimax decision and worst-case cost.
- Use probabilistic reasoning
to find the best expected-case decision and expected cost.
- Characterize the set of all probability distributions for which
the minimax decision and the best expected decision results in the
same choice.
- In a constant-sum game, the costs for any
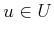 and
and 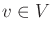 add to yield
add to yield
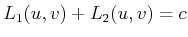 |
(9.96) |
for some constant 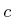 that is independent of
that is independent of 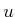 and
and 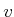 . Show that
any constant-sum game can be transformed into a zero-sum game, and
that saddle point solutions can be found using techniques for the
zero-sum formulation.
. Show that
any constant-sum game can be transformed into a zero-sum game, and
that saddle point solutions can be found using techniques for the
zero-sum formulation.
- Formalize Example 9.7 as a
zero-sum game, and compute security strategies for the players. What
is the expected value of the game?
- Suppose that for two zero-sum games, there
exists some nonzero
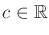 for which the cost matrix of one game
is obtained by multiplying all entries by
for which the cost matrix of one game
is obtained by multiplying all entries by 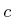 in the cost matrix of
the other. Prove that these two games must have the same
deterministic and randomized saddle points.
in the cost matrix of
the other. Prove that these two games must have the same
deterministic and randomized saddle points.
- In the same spirit as Exercise 11, prove that
two zero-sum games have the same deterministic and randomized saddle
points if
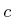 is added to all matrix entries.
is added to all matrix entries.
- Prove that multiple Nash equilibria of a nonzero-sum game
specified by matrices
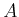 and
and 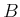 are interchangeable if
are interchangeable if 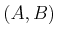 as a
game yields the same Nash equilibria as the game
as a
game yields the same Nash equilibria as the game 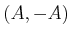 .
.
- Analyze the game of Rock-Paper-Scissors for three players.
For each player, assign a cost of
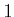 for losing, 0 for a tie, and
for losing, 0 for a tie, and
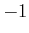 for winning. Specify the cost functions. Is it possible to
avoid regret? Does it have a deterministic Nash equilibrium? Can you
find a randomized Nash equilibrium?
for winning. Specify the cost functions. Is it possible to
avoid regret? Does it have a deterministic Nash equilibrium? Can you
find a randomized Nash equilibrium?
- Compute the randomized equilibrium point for the following
zero-sum game:
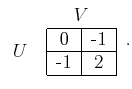 |
(9.97) |
Indicate the randomized strategies for the players and the resulting
expected value of the game.
Implementations
- Consider estimating the value of an unknown parameter,
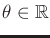 . The prior probability density is a normal,
. The prior probability density is a normal,
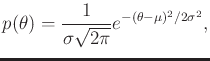 |
(9.98) |
with 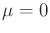 and
and
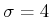 . Suppose that a sequence,
. Suppose that a sequence, 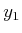 ,
,
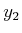 ,
,  ,
, 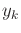 , of
, of  observations is made and that each
observations is made and that each
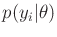 is a normal density with
is a normal density with
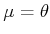 and
and
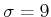 . Suppose that
. Suppose that 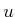 represents your guess of the parameter value.
The task is select
represents your guess of the parameter value.
The task is select 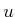 to minimize the expectation of the cost,
to minimize the expectation of the cost,
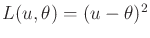 . Suppose that the ``true'' value of
. Suppose that the ``true'' value of
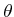 is
is 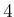 . Determine the
. Determine the 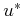 , the minimal action with respect
to the expected cost after observing:
, the minimal action with respect
to the expected cost after observing: 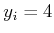 for every
for every
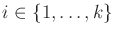 .
.
- Determine
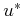 for
for 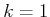 .
.
- Determine
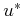 for
for 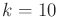 .
.
- Determine
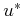 for
for 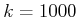 .
.
This experiment is not very realistic because the observations should
be generated by sampling from the normal density,
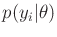 .
Repeat the exercise using values drawn with the normal density,
instead of
.
Repeat the exercise using values drawn with the normal density,
instead of 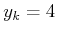 , for each
, for each  .
.
- Implement an algorithm that computes a randomized saddle point
for zero-sum games. Assume that one player has no more than two
actions and the other may have any finite number of actions.
- Suppose that a
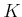 -stage decision-making problem is defined using
multiple objectives. There is a finite state space
-stage decision-making problem is defined using
multiple objectives. There is a finite state space  and a finite
action set
and a finite
action set 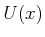 for each
for each 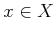 . A state transition equation,
. A state transition equation,
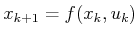 , gives the next state from a current state and
input. There are
, gives the next state from a current state and
input. There are 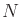 cost functionals of the form
cost functionals of the form
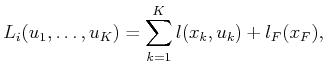 |
(9.99) |
in which 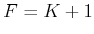 . Assume that
. Assume that
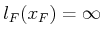 if
if
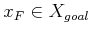 (for some goal region
(for some goal region
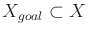 ) and
) and
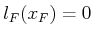 otherwise. Assume that there is no termination action (which
simplifies the problem). Develop a value-iteration approach that
finds the complete set of Pareto-optimal plans efficiently as
possible. If two or more plans produce the same cost vector, then
only one representative needs to be returned.
otherwise. Assume that there is no termination action (which
simplifies the problem). Develop a value-iteration approach that
finds the complete set of Pareto-optimal plans efficiently as
possible. If two or more plans produce the same cost vector, then
only one representative needs to be returned.
Steven M LaValle
2020-08-14