If
 , the security strategies are called a
saddle point, and
, the security strategies are called a
saddle point, and
 is called the value of the game. If this occurs, the order of the
is called the value of the game. If this occurs, the order of the 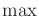 and
and
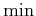 can be swapped without changing the value:
can be swapped without changing the value:
 |
(9.51) |
A saddle point is sometimes referred to as an equilibrium
because the players have no incentive to change their choices (because
there is no regret). A saddle point is defined as any
 and
and
 such that
such that
 |
(9.52) |
for all 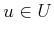 and
and 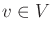 . Note that
. Note that
 . When looking at a matrix game, a saddle point is
found by finding the simple pattern shown in Figure
9.2.
. When looking at a matrix game, a saddle point is
found by finding the simple pattern shown in Figure
9.2.
Figure 9.2:
A saddle point can be detected in a
matrix by finding a value  that is lowest among all elements
in its column and greatest among all elements in its row.
that is lowest among all elements
in its column and greatest among all elements in its row.
 |
Example 9..14 (A Deterministic Saddle Point)
Here is a matrix game that has a saddle point:
 |
(9.53) |
By applying (
9.52) (or using Figure
9.2), the saddle point is obtained when
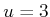
and

. The result is that

. In this case, neither player
has regret after the game is finished.
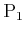
is satisfied because
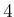
is the lowest cost it could have received, given that
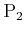
chose the
third column. Likewise,
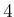
is the highest cost that
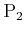
could have
received, given that
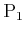
chose the bottom row.

What if there are multiple saddle points in the same game? This may
appear to be a problem because the players have no way to coordinate
their decisions. What if
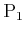 tries to achieve one saddle point
while
tries to achieve one saddle point
while
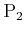 tries to achieve another? It turns out that if there is
more than one saddle point, then there must at least be four, as shown
in Figure 9.3. As soon as we try to make two ``+''
patterns like the one shown in Figure 9.2, they
intersect, and four saddle points are created. Similar behavior
occurs as more saddle points are added.
tries to achieve another? It turns out that if there is
more than one saddle point, then there must at least be four, as shown
in Figure 9.3. As soon as we try to make two ``+''
patterns like the one shown in Figure 9.2, they
intersect, and four saddle points are created. Similar behavior
occurs as more saddle points are added.
Figure 9.3:
A matrix could have more than one
saddle point, which may seem to lead to a coordination problem between
the players. Fortunately, there is no problem, because the same value
will be received regardless of which saddle point is selected by each
player.
 |
Example 9..15 (Multiple Saddle Points)
This game has multiple saddle points and follows the pattern in
Figure
9.3:
 |
(9.54) |
Let
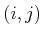
denote the pair of choices for
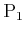
and
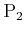
,
respectively. Both
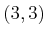
and

are saddle points with value

. What if
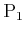
chooses
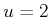
and
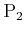
chooses

?
This is not a problem because

is also a saddle point.
Likewise,

is another saddle point. In general, no problems
are caused by the existence of multiple saddle points because the
resulting cost is independent of which saddle point is attempted by
each player.

Steven M LaValle
2020-08-14

![]() , the security strategies are called a
saddle point, and
, the security strategies are called a
saddle point, and
![]() is called the value of the game. If this occurs, the order of the
is called the value of the game. If this occurs, the order of the ![]() and
and
![]() can be swapped without changing the value:
can be swapped without changing the value:
![]() and
and
![]() such that
such that

![]() tries to achieve one saddle point
while
tries to achieve one saddle point
while
![]() tries to achieve another? It turns out that if there is
more than one saddle point, then there must at least be four, as shown
in Figure 9.3. As soon as we try to make two ``+''
patterns like the one shown in Figure 9.2, they
intersect, and four saddle points are created. Similar behavior
occurs as more saddle points are added.
tries to achieve another? It turns out that if there is
more than one saddle point, then there must at least be four, as shown
in Figure 9.3. As soon as we try to make two ``+''
patterns like the one shown in Figure 9.2, they
intersect, and four saddle points are created. Similar behavior
occurs as more saddle points are added.
