
Next: 9.2.4 Examples of Optimal Up: 9.2.3 Making Use of Previous: Nature acts twice
Another extension of Formulation 9.5 is to allow
multiple observations, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , before making a
decision. Each
, before making a
decision. Each ![]() is assumed to belong to an observation space,
is assumed to belong to an observation space,
![]() . A strategy,
. A strategy, ![]() , now depends on all observations:
, now depends on all observations:
| (9.29) |
Under the nondeterministic model,
![]() is specified for each
is specified for each
![]() and
and
![]() . The set
. The set ![]() is replaced by
is replaced by
| (9.30) |
Under the probabilistic model,
![]() is specified instead.
It is often assumed that the observations are conditionally
independent given
is specified instead.
It is often assumed that the observations are conditionally
independent given ![]() . This means for any
. This means for any ![]() ,
, ![]() , and
, and
![]() such that
such that
![]() ,
,
![]() .
The condition
.
The condition
![]() in (9.26) is replaced by
in (9.26) is replaced by
![]() . Applying Bayes' rule, and using the
conditional independence of the
. Applying Bayes' rule, and using the
conditional independence of the ![]() 's given
's given ![]() , yields
, yields
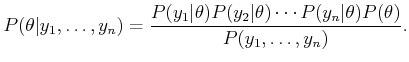 |
(9.31) |
Conditional independence allows a dramatic simplification that avoids
the full specification of
![]() . Sometimes the conditional
independence assumption is used when it is incorrect, just to exploit
this simplification. Therefore, a method that uses conditional
independence of observations is often called naive Bayes.
. Sometimes the conditional
independence assumption is used when it is incorrect, just to exploit
this simplification. Therefore, a method that uses conditional
independence of observations is often called naive Bayes.
Steven M LaValle 2020-08-14