
Next: Piecewise-smooth vector fields Up: 8.3.1 Vector Fields on Previous: Vector fields as velocity
If a vector field ![]() is given, then a velocity vector is defined at
each point using (8.10). Imagine a point that starts
at some
is given, then a velocity vector is defined at
each point using (8.10). Imagine a point that starts
at some
![]() at time
at time ![]() and then moves according to
the velocities expressed in
and then moves according to
the velocities expressed in ![]() . Where should it travel? Its
trajectory starting from
. Where should it travel? Its
trajectory starting from ![]() can be expressed as a function
can be expressed as a function
![]() , in which the domain is a time
interval,
, in which the domain is a time
interval,
![]() . A trajectory represents an integral
curve (or solution trajectory) of the differential equations
with initial condition
. A trajectory represents an integral
curve (or solution trajectory) of the differential equations
with initial condition
![]() if
if
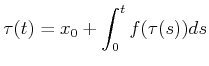 |
(8.15) |
A basic result from differential equations is that a unique integral
curve exists to
![]() if
if ![]() is smooth. An alternative
condition is that a unique solution exists if
is smooth. An alternative
condition is that a unique solution exists if ![]() satisfies a
Lipschitz condition. This means that there exists some constant
satisfies a
Lipschitz condition. This means that there exists some constant
![]() such that
such that
Steven M LaValle 2020-08-14