Even though multiple-robot motion planning can be handled like any
other motion planning problem, there are several reasons to study it
separately:
- The motions of the robots can be decoupled in many interesting
ways. This leads to several interesting methods that first develop
some kind of partial plan for the robots independently, and then
consider the plan interactions to produce a solution. This idea is
referred to as decoupled planning.
- The part of
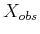 due to robot-robot collisions has a
cylindrical structure, depicted in Figure 7.6, which
can be exploited to make more efficient planning algorithms. Each
due to robot-robot collisions has a
cylindrical structure, depicted in Figure 7.6, which
can be exploited to make more efficient planning algorithms. Each
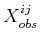 defined by (7.8) depends only on two
robots. A point,
defined by (7.8) depends only on two
robots. A point,
 , is in
, is in 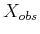 if there
exists
if there
exists  such that
such that
 and
and
 , regardless of the configurations of the
other
, regardless of the configurations of the
other  robots. For some decoupled methods, this even implies
that
robots. For some decoupled methods, this even implies
that 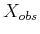 can be completely characterized by 2D projections, as
depicted in Figure 7.9.
can be completely characterized by 2D projections, as
depicted in Figure 7.9.
- If optimality is important, then a unique set of issues arises
for the case of multiple robots. It is not a standard optimization
problem because the performance of each robot has to be optimized.
There is no clear way to combine these objectives into a single
optimization problem without losing some critical information. It
will be explained in Section 7.7.2 that Pareto optimality
naturally arises as the appropriate notion of optimality for
multiple-robot motion planning.
Figure 7.6:
The set
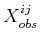 and its cylindrical structure on
and its cylindrical structure on  .
.
 |
Steven M LaValle
2020-08-14
