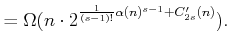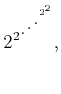6.5.2 Davenport-Schinzel Sequences
Davenport-Schinzel sequences provide a powerful characterization of
the structure that arises from the lower or upper envelope of a
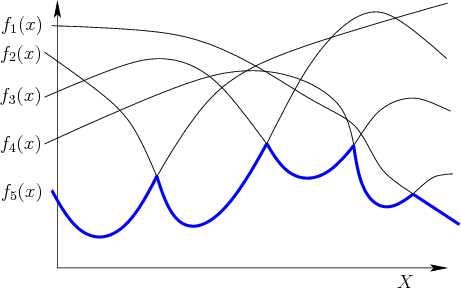
collection of functions. The lower envelope of five functions
is depicted in Figure 6.42. Such envelopes arise in
many problems throughout computational geometry, including many motion
planning problems. They are an important part of the design and
analysis of many modern algorithms, and the resulting algorithm's time
complexity usually involves terms that follow directly from the
sequences. Therefore, it is worthwhile to understand some of the
basics before interpreting some of the results of Section
6.5.3. Much more information on Davenport-Schinzel sequences
and their applications appears in [866]. The brief
introduction presented here is based on [865].
Figure 6.42:
The lower envelope of a collection
of functions.
 |
For positive integers 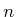 and
and 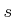 , an
, an 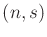 Davenport-Schinzel
sequence is a sequence
Davenport-Schinzel
sequence is a sequence
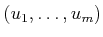 composed from a set of
composed from a set of 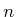 symbols such that:
symbols such that:
- The same symbol may not appear consecutively in the sequence.
In other words,
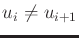 for any
for any 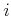 such that
such that
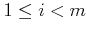 .
.
- The sequence does not contain any alternating subsequence that
uses two symbols and has length
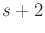 . A subsequence can be formed by
deleting any elements in the original sequence. The condition can be
expressed as: There do not exist
. A subsequence can be formed by
deleting any elements in the original sequence. The condition can be
expressed as: There do not exist 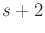 indices
indices
 for which
for which
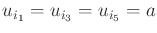 and
and
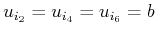 , for some symbols
, for some symbols 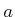 and
and 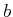 .
.
As an example, an 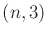 sequence cannot appear as
sequence cannot appear as
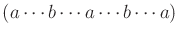 , in which each
, in which each  is filled in with
any sequence of symbols. Let
is filled in with
any sequence of symbols. Let
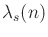 denote the maximum
possible length of an
denote the maximum
possible length of an 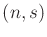 Davenport-Schinzel sequence.
Davenport-Schinzel sequence.
The connection between Figure 6.42 and these sequences
can now be explained. Consider the sequence of function indices that
visit the lower envelope. In the example, this sequence is
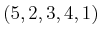 . Suppose it is known that each pair of functions
intersects in at most
. Suppose it is known that each pair of functions
intersects in at most 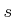 places. If there are
places. If there are 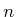 real-valued
continuous functions, then the sequence of function indices must be an
real-valued
continuous functions, then the sequence of function indices must be an
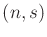 Davenport-Schinzel sequence. It is amazing that such
sequences cannot be very long. For a fixed
Davenport-Schinzel sequence. It is amazing that such
sequences cannot be very long. For a fixed 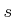 , they are close to
being linear.
, they are close to
being linear.
The standard bounds for Davenport-Schinzel sequences are
[865]6.9
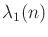 |
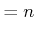 |
(6.32) |
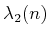 |
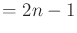 |
(6.33) |
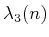 |
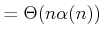 |
(6.34) |
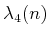 |
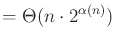 |
(6.35) |
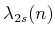 |
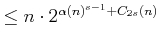 |
(6.36) |
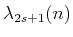 |
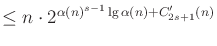 |
(6.37) |
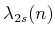 |
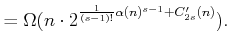 |
(6.38) |
In the expressions above 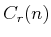 and
and
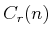 are terms that
are smaller than their leading exponents. The
are terms that
are smaller than their leading exponents. The 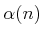 term is the
inverse Ackerman function, which is an extremely slow-growing function
that appears frequently in algorithms. The Ackerman function is
defined as follows. Let
term is the
inverse Ackerman function, which is an extremely slow-growing function
that appears frequently in algorithms. The Ackerman function is
defined as follows. Let
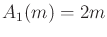 and
and
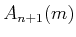 represent
represent 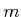 applications of
applications of 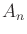 . Thus,
. Thus, 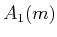 performs doubling,
performs doubling, 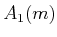 performs exponentiation, and
performs exponentiation, and 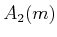 performs tower
exponentiation, which makes a stack of
performs tower
exponentiation, which makes a stack of 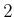 's,
's,
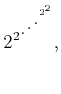 |
(6.39) |
that has height 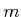 . The Ackerman function is defined as
. The Ackerman function is defined as
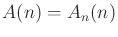 . This function grows so fast that
. This function grows so fast that 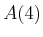 is already an
exponential tower of
is already an
exponential tower of 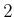 's that has height
's that has height 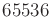 . Thus, the
inverse Ackerman function,
. Thus, the
inverse Ackerman function, 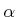 , grows very slowly. If
, grows very slowly. If 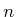 is less than or equal to an exponential tower of
is less than or equal to an exponential tower of 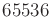
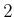 's, then
's, then
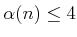 . Even when it appears in exponents of the
Davenport-Schinzel bounds, it does not represent a significant growth
rate.
. Even when it appears in exponents of the
Davenport-Schinzel bounds, it does not represent a significant growth
rate.
Example 6..9 (Lower Envelope of Line Segments)
One interesting application of Davenport-Schinzel applications is to
the lower envelope
of a set of line segments in
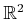
. Since
segments in general position may appear multiple times along the lower
envelope, the total number of edges is
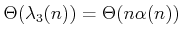
, which is higher than one would obtain from
infinite lines. There are actually arrangements of segments in
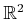
that reach this bound; see [
866].

Steven M LaValle
2020-08-14

![]() and
and ![]() , an
, an ![]() Davenport-Schinzel
sequence is a sequence
Davenport-Schinzel
sequence is a sequence
![]() composed from a set of
composed from a set of ![]() symbols such that:
symbols such that:
![]() . Suppose it is known that each pair of functions
intersects in at most
. Suppose it is known that each pair of functions
intersects in at most ![]() places. If there are
places. If there are ![]() real-valued
continuous functions, then the sequence of function indices must be an
real-valued
continuous functions, then the sequence of function indices must be an
![]() Davenport-Schinzel sequence. It is amazing that such
sequences cannot be very long. For a fixed
Davenport-Schinzel sequence. It is amazing that such
sequences cannot be very long. For a fixed ![]() , they are close to
being linear.
, they are close to
being linear.