The most important family of metrics over
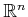 is given for any
is given for any  as
as
 |
(5.1) |
For each value of 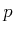 , (5.1) is called an
, (5.1) is called an 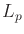 metric (pronounced ``el pee''). The three most common cases are
metric (pronounced ``el pee''). The three most common cases are
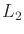 : The Euclidean metric, which is the familiar
Euclidean distance in
: The Euclidean metric, which is the familiar
Euclidean distance in
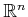 .
.
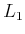 : The Manhattan metric, which is often nicknamed
this way because in
: The Manhattan metric, which is often nicknamed
this way because in
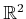 it corresponds to the length of a path
that is obtained by moving along an axis-aligned grid. For example,
the distance from
it corresponds to the length of a path
that is obtained by moving along an axis-aligned grid. For example,
the distance from 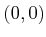 to
to  is
is 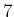 by traveling ``east two
blocks'' and then ``north five blocks''.
by traveling ``east two
blocks'' and then ``north five blocks''.
 : The
: The  metric must actually be
defined by taking the limit of (5.1) as
metric must actually be
defined by taking the limit of (5.1) as 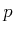 tends to
infinity. The result is
tends to
infinity. The result is
 |
(5.2) |
which seems correct because the larger the value of 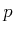 , the more the
largest term of the sum in (5.1) dominates.
, the more the
largest term of the sum in (5.1) dominates.
An 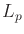 metric can be derived from a norm on a vector space. An
metric can be derived from a norm on a vector space. An
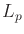 norm over
norm over
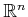 is defined as
is defined as
 |
(5.3) |
The case of  is the familiar definition of the magnitude of a
vector, which is called the Euclidean norm. For example, assume
the vector space is
is the familiar definition of the magnitude of a
vector, which is called the Euclidean norm. For example, assume
the vector space is
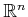 , and let
, and let  be the standard
Euclidean norm. The
be the standard
Euclidean norm. The 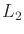 metric is
metric is
 . Any
. Any 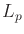 metric can be written in terms of a vector subtraction, which is
notationally convenient.
metric can be written in terms of a vector subtraction, which is
notationally convenient.
Steven M LaValle
2020-08-14

![]() is given for any
is given for any ![]() as
as