Simply connected

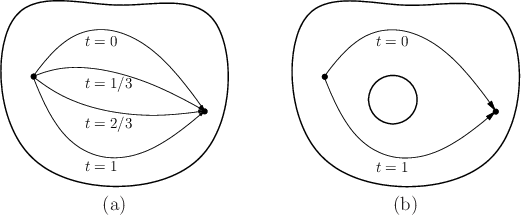
Now that the notion of connectedness has been established, the next step is to express different kinds of connectivity. This may be done by using the notion of homotopy, which can intuitively be considered as a way to continuously ``warp'' or ``morph'' one path into another, as depicted in Figure 4.6a.

Figure 4.6: (a) Homotopy continuously warps one path into another. (b) The image of the path cannot be continuously warped over a hole in ${\mathbb{R}}^2$ because it causes a discontinuity. In this case, the two paths are not homotopic.

Two paths $\tau_{1}$ and $\tau_{2}$ are called homotopic (with endpoints fixed) if there exists a continuous function $h : [0,1] \times [0,1] \rightarrow X$ for which the following four conditions are met:

1. (Start with first path) $h(s,0) = \tau_{1}(s)$ for all $s \in [0,1]$ .
2. (End with second path) $h(s,1) = \tau_{2}(s)$ for all $s \in [0,1]$ .
3. (Hold starting point fixed) $h(0,t) = h(0,0)$ for all $t \in [0,1]$ .
4. (Hold ending point fixed) $h(1,t) = h(1,0)$ for all $t \in [0,1]$ .

The parameter $t$ can be interpreted as a knob that is turned to gradually deform the path from $\tau_1$ into $\tau_2$. The first two conditions indicate that $t=0$ yields $\tau_{1}$ and $t=1$ yields $\tau_{2}$, respectively. The remaining two conditions indicate that the path endpoints are held fixed.

During the warping process, the path image cannot make a discontinuous jump. In ${\mathbb{R}}^2$, this prevents it from moving over holes, such as the one shown in Figure 4.6b. The key to preventing homotopy from jumping over some holes is that $h$ must be continuous. In higher dimensions, however, there are many different kinds of holes. For the case of ${\mathbb{R}}^3$, for example, suppose the space is like a block of Swiss cheese that contains air bubbles. Homotopy can go around the air bubbles, but it cannot pass through a hole that is drilled through the entire block of cheese. Air bubbles and other kinds of holes that appear in higher dimensions can be characterized by generalizing homotopy to the warping of higher dimensional surfaces, as opposed to paths [439].

It is straightforward to show that homotopy defines an equivalence relation on the set of all paths from some $x_1 \in X$ to some $x_2 \in X$. The resulting notion of ``equivalent paths'' appears frequently in motion planning, control theory, and many other contexts. Suppose that $X$ is path connected. If all paths fall into the same equivalence class, then $X$ is called simply connected; otherwise, $X$ is called multiply connected.