The homogeneous transformation matrix 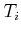 will be constructed by combining two simpler transformations. The
transformation
will be constructed by combining two simpler transformations. The
transformation
 |
(3.54) |
causes a rotation of 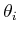 about the
about the 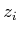 -axis, and a
translation of
-axis, and a
translation of 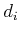 along the
along the 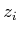 -axis. Notice that the rotation
by
-axis. Notice that the rotation
by 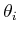 and translation by
and translation by 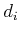 commute because both operations
occur with respect to the same axis,
commute because both operations
occur with respect to the same axis, 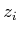 . The combined operation of
a translation and rotation with respect to the same axis is referred
to as a screw (as in the motion of a
screw through a nut). The effect of
. The combined operation of
a translation and rotation with respect to the same axis is referred
to as a screw (as in the motion of a
screw through a nut). The effect of  can thus be considered as a
screw about the
can thus be considered as a
screw about the 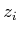 -axis. The second transformation is
-axis. The second transformation is
 |
(3.55) |
which can be considered as a screw about the 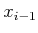 -axis. A
rotation of
-axis. A
rotation of
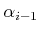 about the
about the 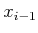 -axis and a translation
of
-axis and a translation
of 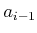 are performed.
are performed.
Steven M LaValle
2020-08-14
