
Next: Sampling rate Up: 8.3.2 Numerical simulation Previous: Degrees of freedom Contents Index
We now introduce some basic differential equations to model motions. The resulting description is often called a dynamical system. The first step is to describe rigid body velocities in terms of state. Returning to models that involve one or more rigid bodies, the state corresponds to a finite number of parameters. Let
| (8.18) |
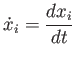 |
(8.19) |
To obtain the state at any time ![]() , the velocities need to be integrated over time. Following (8.4), the integration of each state variable determines the value at time
, the velocities need to be integrated over time. Following (8.4), the integration of each state variable determines the value at time ![]() :
:
Two main problems arise with (8.20):
Steven M LaValle 2020-11-11