
Next: 15.4.2.4 The Frobenius Theorem Up: 15.4.2 Determining Whether a Previous: 15.4.2.2 Distributions
The key to establishing whether a system is nonholonomic is to
construct motions that combine the effects of two action variables,
which may produce motions in a direction that seems impossible from
the system distribution. To motivate the coming ideas, consider the
differential-drive model from (15.54). Apply the
following piecewise-constant action trajectory over the interval
![]() :
:
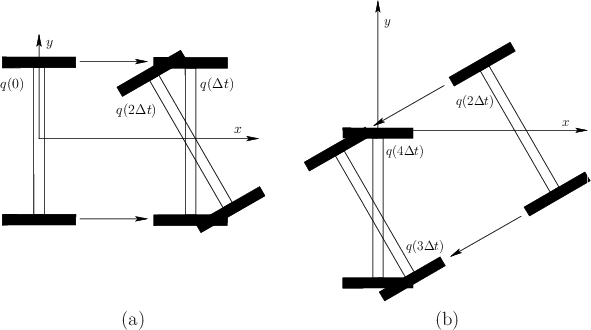 |
The result of all four motion primitives in succession from
![]() is shown in Figure 15.16. It is fun to try
this at home with an axle and two wheels (Tinkertoys work well, for
example). The result is that the differential drive moves
sideways!15.9 From the
transition equation (15.54) such motions appear
impossible. This is a beautiful property of nonlinear systems. The
state may wiggle its way in directions that do not seem possible. A
more familiar example is parallel parking a car.
It is known that a car cannot directly move sideways; however, some
wiggling motions can be performed to move it sideways into a tight
parking space. The actions we perform while parking resemble the
primitives in (15.71).
is shown in Figure 15.16. It is fun to try
this at home with an axle and two wheels (Tinkertoys work well, for
example). The result is that the differential drive moves
sideways!15.9 From the
transition equation (15.54) such motions appear
impossible. This is a beautiful property of nonlinear systems. The
state may wiggle its way in directions that do not seem possible. A
more familiar example is parallel parking a car.
It is known that a car cannot directly move sideways; however, some
wiggling motions can be performed to move it sideways into a tight
parking space. The actions we perform while parking resemble the
primitives in (15.71).
Algebraically, the motions of (15.71) appear to be checking
for commutativity. Recall from Section 4.2.1 that a
group ![]() is called commutative (or
Abelian) if
is called commutative (or
Abelian) if ![]() for any
for any ![]() . A commutator
is a group element of the form
. A commutator
is a group element of the form
![]() . If the group is
commutative, then
. If the group is
commutative, then
![]() (the identity element) for any
(the identity element) for any
![]() . If a nonidentity element of
. If a nonidentity element of ![]() is produced by the
commutator, then the group is not commutative. Similarly, if the
trajectory arising from (15.71) does not form a loop (by
returning to the starting point), then the motion primitives do not
commute. Therefore, a sequence of motion primitives in
(15.71) will be referred to as the commutator motion.
It will turn out that if the commutator motion cannot produce any
velocities not allowed by the system distribution, then the system is
completely integrable. This means that if we are trapped on a
surface, then it is impossible to leave the surface by using
commutator motions.
is produced by the
commutator, then the group is not commutative. Similarly, if the
trajectory arising from (15.71) does not form a loop (by
returning to the starting point), then the motion primitives do not
commute. Therefore, a sequence of motion primitives in
(15.71) will be referred to as the commutator motion.
It will turn out that if the commutator motion cannot produce any
velocities not allowed by the system distribution, then the system is
completely integrable. This means that if we are trapped on a
surface, then it is impossible to leave the surface by using
commutator motions.
Now generalize the differential drive to any driftless control-affine system that has two action variables:
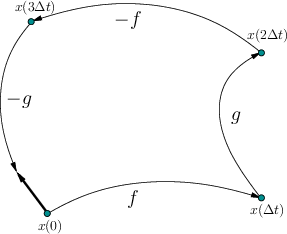 |
Suppose that the commutator motion (15.71) is applied to
(15.72) as shown in Figure 15.17. Determining
the resulting motion requires some general computations, as opposed to
the simple geometric arguments that could be made for the differential
drive. If would be convenient to have an expression for the velocity
obtained in the limit as ![]() approaches zero. This can be
obtained by using Taylor series arguments. These are simplified by
the fact that the action history is piecewise constant.
approaches zero. This can be
obtained by using Taylor series arguments. These are simplified by
the fact that the action history is piecewise constant.
The coming derivation will require an expression for ![]() under
the application of a constant action. For each action, a vector field
of the form
under
the application of a constant action. For each action, a vector field
of the form
![]() is obtained. Upon differentiation, this
yields
is obtained. Upon differentiation, this
yields
Now the state trajectory under the application of (15.71)
will be determined using the Taylor series, which was given in
(14.17). The state trajectory that results from the
first motion primitive ![]() can be expressed as
can be expressed as
The idea of substituting previous Taylor series expansions as they are needed can be repeated for the remaining two motion primitives. The Taylor series expansion for the result after the third primitive is
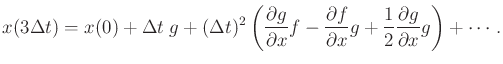 |
(15.78) |
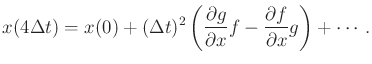 |
(15.79) |
By applying (15.81), the Lie bracket ![]() is
is
As a simple example, recall the nonholonomic integrator (13.43). In the linear-algebra form, the system is
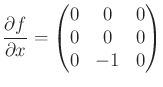 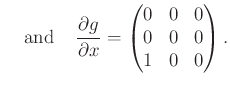 |
(15.84) |
![]()
Steven M LaValle 2020-08-14