Completing the state transition equation

Assume that the body frame of ${\cal A}$ aligns with the principle axes. The remaining six equations of motion can finally be given in a nice form. Using (13.99), the expression (13.98) reduces to [681]

$$\begin{split}\begin{pmatrix}N_1(u) \\ N_2(u) \\ N_3(u) \end{p... ...ix}\omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix} . \end{split}$$ (13.100)

Multiplying out (13.100) yields

$$\begin{split}{N}_1(u) & = I_{11} {\dot \omega}_1 + (I_{33}-I_... ...dot \omega}_3 + (I_{22}-I_{11}) \omega_1 \omega_2 . \end{split}$$ (13.101)

To prepare for the state transition equation form, solving for ${\dot \omega}$ yields

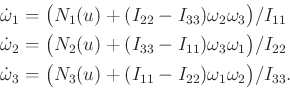$$\begin{split}{\dot \omega}_1 & = \big({N}_1(u) + (I_{22}-I_{3... ...) + (I_{11}-I_{22}) \omega_1 \omega_2\big)/I_{33} . \end{split}$$ (13.102)

One final complication is that $\omega$ needs to be related to angles that are used to express an element of $SO(3)$. The mapping between these depends on the particular parameterization of $SO(3)$. Suppose that quaternions of the form $(a,b,c,d)$ are used to express rotation. Recall that $a$ can be recovered once $b$, $c$, and $d$ are given using $a^2 + b^2 + c^2 + d^2 = 1$. The relationship between $\omega$ and the time derivatives of the quaternion components is obtained by using (13.84) (see [690], p. 433):

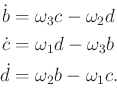$$\begin{split}{\dot b}& = \omega_3 c - \omega_2 d \\ {\dot c}&... ...ega_3 b \\ {\dot d}& = \omega_2 b - \omega_1 c . \\ \end{split}$$ (13.103)

This finally completes the specification of ${\dot x}= f(x,u)$, in which

$$x = (p_1,p_2,p_3,v_1,v_2,v_3,b,c,d,\omega_1,\omega_2,\omega_3)$$ (13.104)

is a twelve-dimensional phase vector. For convenience, the full specification of the state transition equation is

$${\dot p}_1 = v_1 \qquad {\dot b} = \omega_3 c - \omega_2 d$$

$${\dot p}_2 = v_2 \qquad {\dot c} = \omega_1 d - \omega_3 b$$

$${\dot p}_3 = v_3 \qquad {\dot d} = \omega_2 b - \omega_1 c$$ (13.105)

$${\dot v}_1 = {F}_1(u)/{m} \qquad {\dot \omega}_1 = \big(N_1(u) + (I_{22}-I_{33}) \omega_2 \omega_3\big)/I_{11}$$

$${\dot v}_2 = {F}_2(u)/{m} \qquad {\dot \omega}_2 = \big(N_2(u) + (I_{33}-I_{11}) \omega_3 \omega_1\big)/I_{22}$$

$${\dot v}_3 = {F}_3(u)/{m} \qquad {\dot \omega}_3 = \big(N_3(u) + (I_{11}-I_{22}) \omega_1 \omega_2\big)/I_{33} .$$

The relationship between inertia matrices and ellipsoids is actually much deeper than presented here. The kinetic energy due to rotation only is elegantly expressed as

$$T = \begin{matrix}\frac{1}{2} \end{matrix} \omega^T I \omega .$$ (13.106)

A fascinating interpretation of rotational motion in the absence of external forces was given by Poinsot [39,681]. As the body rotates, its motion is equivalent to that of the inertia ellipsoid, given by (13.106), rolling (without sliding) down a plane with normal vector $I \omega$ in ${\mathbb{R}}^3$.