
Next: Inertia matrix Up: 13.3.3 Motion of a Previous: The rotational part
To express the change in the moment of momentum in detail, the
concept of a differential rotation is needed. In the plane, it is
straightforward to define
![]() ; however, for
; however, for ![]() ,
it is more complicated. One choice is to define derivatives with
respect to yaw-pitch-roll variables, but this leads to distortions and
singularities, which are problematic for the Newton-Euler formulation.
Instead, a differential rotation is defined as shown in Figure
13.11. Let
,
it is more complicated. One choice is to define derivatives with
respect to yaw-pitch-roll variables, but this leads to distortions and
singularities, which are problematic for the Newton-Euler formulation.
Instead, a differential rotation is defined as shown in Figure
13.11. Let ![]() denote a unit vector in
denote a unit vector in
![]() , and let
, and let
![]() denote a rotation that is analogous to the 2D case. Let
denote a rotation that is analogous to the 2D case. Let
![]() denote the angular velocity vector,
denote the angular velocity vector,
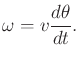 |
(13.83) |
Steven M LaValle 2020-08-14