Competitive ratios

A popular way to evaluate algorithms that utilize different information has emerged from the algorithms community. The idea is to compute a competitive ratio, which places an on-line algorithm in competition with an algorithm that receives more information [674,892]. The idea can generally be applied to plans. First a cost is formulated, such as the total distance that the robot travels to solve a navigation task. A competitive ratio can then be defined as

$$\max_{e \in E} {\mbox{Cost of executing the plan that does not kn... ...dvance.} \over \mbox{Cost of executing the plan that knows $e$\ in advance} } .$$ (12.28)

The maximum is taken over all $e \in E$, which is usually an infinite set, as in the case of the bug algorithms. A competitive ratio for a navigation problem can be made by comparing the optimal distance to the total distance traveled by the robot during the execution of the on-line algorithm. Since $E$ is infinite, many plans fail to produce a finite competitive ratio. The bug algorithms, while elegant, represent such an example. Imagine a goal that is very close, but a large obstacle boundary needs to be explored. An obstacle boundary can be made arbitrarily large while making the optimal distance to the goal very small. When evaluated in (12.28), the result over all environments is unbounded. In some contexts, the ratio may still be useful if expressed as a function of the representation. For example, if $E$ is a polygon with $n$ edges, then an $O(\sqrt n)$ competitive ratio means that (12.28) is bounded over all $n$ by $c \sqrt n$ for some $c \in {\mathbb{R}}$. For competitive ratio analysis in the context of bug algorithms, see [375].

Figure 12.26: (a) A lost cow must find its way to the gate, but it does not know in which direction the gate lies. (b) If there is no bound on the distance to the gate, then a doubling spiral strategy works well, producing a competitive ratio of $9$.

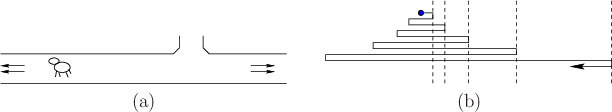A nice illustration of competitive ratio analysis and issues is provided by the lost-cow problem [60]. As shown in Figure 12.26a, a short-sighted cow is following along an infinite fence and wants to find the gate. This makes a convenient one-dimensional planning problem. If the location of the gate is given, then the cow can reach it by traveling directly. If the cow is told that the gate is exactly distance $1$ away, then it can move one unit in one direction and return to try the other direction if the gate has not been found. The competitive ratio in this case (the set of environments corresponds to all gate placements) is $3$. What if the cow is told only that the gate is at least distance 1 away? In this case, the best strategy is a spiral search, which is to zig-zag back and forth while iteratively doubling the distance traveled in each direction, as shown in Figure 12.26b. In other words: left one unit, right one unit, left two units, right two units, left four units, and so on. The competitive ratio for this strategy turns out to be $9$, which is optimal. This approach resembles iterative deepening, which was covered in Section 2.2.2.