Algorithms for maze searching

A fascinating example of using an I-map to dramatically reduce the I-space was given a long time ago by Blum and Kozen [119]. Map building requires space that is linear in the number of tiles; however, it is possible to ensure that the environment has been systematically searched using much less space. For 2D grid environments, the searching problem can be solved without maintaining a complete map. It must systematically visit every tile; however, this does not imply that it must remember all of the places that it has visited. It is important only to ensure that the robot does not become trapped in an infinite loop before covering all tiles. It was shown in [119] that any maze can be searched using space that is only logarithmic in the number of tiles. This implies that many different environments have the same representation in the machine. Essentially, an I-map was developed that severely collapses ${\cal I}_{ndet}$ down to a smaller derived I-space.

Assume that the robot motion model is the same as has been given so far in this section; however, no map of the environment is initially given. Whatever direction the robot is facing initially can be declared to be north without any harm. It is assumed that any planar 2D grid is possible; therefore, there are identical maps for each of the four orientations. The north direction of one of these maps might be mislabeled by arbitrarily declaring the initial direction to be north, but this is not critical for the coming approach. It is assumed that the robot is a finite automaton that carries a binary counter. The counter will be needed because it can store values that are arbitrarily large, which is not possible for the automaton alone.

To keep the robot from wandering around in circles forever, two important pieces of information need to be maintained:

1. The latitude, which is the number of tiles in the north direction from the robot's initial position.
2. When a loop path is executed, it needs to know its orientation, which means whether the loop travels clockwise or counterclockwise.

Both of these can be computed from the history I-state, which takes the same form as in (12.12), except in the current setting, $X$ is given by (12.23) and $E$ is the set of all bounded environments (bounded means that the white tiles can be contained in a large rectangle). From the history I-state, let ${\tilde{u}}^\prime_k$ denote the subsequence of the action history that corresponds to actions that produce motions. The latitude, $l({\tilde{u}}^\prime_k)$, can be computed by counting the number of actions that produce motions in the north direction and subtracting those that produce motions in the south direction. The loop orientation can be determined by angular odometry (which is equivalent to having a compass in this problem [286]). Let the value $r({\tilde{u}}^\prime_k)$ give the number of right turns in ${\tilde{u}}^\prime_k$ minus the number of left turns in ${\tilde{u}}^\prime_k$. Note that making four rights yields a clockwise loop and $r({\tilde{u}}^\prime_k) = 4$. Making four lefts yields a counterclockwise loop and $r({\tilde{u}}^\prime_k) = -4$. In general, it can be shown that for any loop path that does not intersect itself, either $r({\tilde{u}}^\prime_k) = 4$, which means that it travels clockwise, or $r({\tilde{u}}^\prime_k) = -4$, which means that it travels counterclockwise.

It was stated that a finite automaton and a binary counter are needed. The counter is used to keep track of $l({\tilde{u}}^\prime_k)$ as the robot moves. It turns out that an additional counter is not needed to measure the angular odometry because the robot can instead perform mod-3 arithmetic when counting right and left turns. If the result is $r({\tilde{u}}^\prime_k) = 1 \mod 3$ after forming a loop, then the robot traveled counterclockwise. If the result is $r({\tilde{u}}^\prime_k) = 2 \mod 3$, then the robot traveled clockwise. This observation avoids using an unlimited number of bits, contrary to the case of maintaining latitude. The construction so far can be viewed as part of an I-map that maps the history I-states into a much smaller derived I-space.

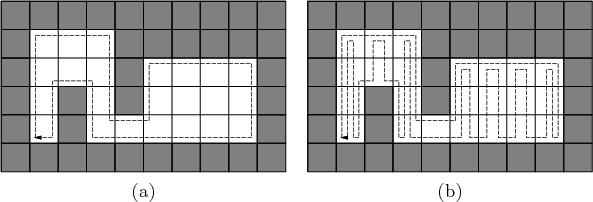
The plan will be described in terms of the example shown in Figure 12.14. For any environment, there are obstacles in the interior (this example has six), and there is an outer boundary. Using the latitude and orientation information, a unique point can be determined on the boundary of each obstacle and on the outer boundary. The unique point is defined as the westernmost vertex among the southernmost vertices of the obstacle. These are shown by small discs in Figure 12.15. By using the latitude and orientation information, the unique point can always be found (see Exercise 4).

To solve the problem, the robot moves to a boundary and traverses it by performing wall following. The robot can use its sensing information to move in a way that keeps the wall to its left. Assuming that the robot can always detect a unique point along the boundary, it can imagine that the obstacles are connected as shown in Figure 12.15. There is a fictitious thin obstacle that extends southward from each unique point. This connects the obstacles together in a way that appears to be an extension of the outer boundary. In other words, imagine that the obstacles are protruding from the walls, as opposed to ``floating'' in the interior. By refusing to cross these fictitious obstacles, the robot moves around the boundary of all obstacles in a single closed-loop path. The strategy so far does not ensure that every cell will be visited. Therefore, the modification shown in Figure 12.16 is needed to ensure that every tile is visited by zig-zag motions. It is interesting to compare the solution to the spanning-tree coverage planning approach in Section 7.6, which assumed a complete map was given and the goal was to optimize the distance traveled.

If there is some special object in the environment that can be detected when reached by the robot, then the given strategy is always guaranteed to find it, even though at the end, it does not even have a map!

The resulting approach can be considered as an information-feedback plan on the I-space. In this sense, Blum and Kozen were the ``planner'' that found a plan that solves any problem. Alternative plans do not need to be computed from the problem data because the plan can handle all possible environments without modification. This is the power of working directly with an I-space over the set of environments, as opposed to requiring state estimation.

Figure 12.14: An example that has six obstacles.

Figure 12.15: The obstacles are connected together by extending a thin obstacle downward from their unique points.

Figure 12.16: (a) A clockwise loop produced by wall following. (b) An alternative loop that visits all of the tiles in the interior.