Now that the group of rotations, 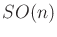 , is characterized, the next
step is to allow both rotations and translations. This corresponds to
the set of all
, is characterized, the next
step is to allow both rotations and translations. This corresponds to
the set of all
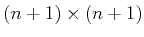 transformation matrices of the
form
transformation matrices of the
form
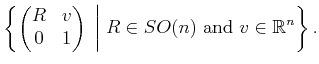 |
(4.16) |
This should look like a generalization of (3.52) and
(3.56), which were for 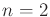 and
and 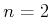 , respectively.
The
, respectively.
The 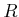 part of the matrix achieves rotation of an
part of the matrix achieves rotation of an  -dimensional
body in
-dimensional
body in
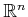 , and the
, and the 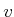 part achieves translation of the same
body. The result is a group,
part achieves translation of the same
body. The result is a group, 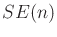 , which is called the
special Euclidean group. As a topological space,
, which is called the
special Euclidean group. As a topological space, 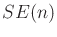 is
homeomorphic to
is
homeomorphic to
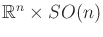 , because the rotation matrix and
translation vectors may be chosen independently. In the case of
, because the rotation matrix and
translation vectors may be chosen independently. In the case of
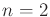 , this means
, this means 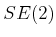 is homeomorphic to
is homeomorphic to
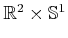 ,
which verifies what was stated at the beginning of this section.
Thus, the C-space of a 2D rigid body that can translate and rotate in
the plane is
,
which verifies what was stated at the beginning of this section.
Thus, the C-space of a 2D rigid body that can translate and rotate in
the plane is
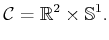 |
(4.17) |
To be more precise,
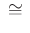 should be used in the place of
should be used in the place of 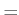 to
indicate that
to
indicate that  could be any space homeomorphic to
could be any space homeomorphic to
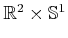 ; however, this notation will mostly be avoided.
; however, this notation will mostly be avoided.
Steven M LaValle
2020-08-14

![]() , is characterized, the next
step is to allow both rotations and translations. This corresponds to
the set of all
, is characterized, the next
step is to allow both rotations and translations. This corresponds to
the set of all
![]() transformation matrices of the
form
transformation matrices of the
form