
Next: 3.4 Transforming Kinematic Trees Up: 3.3.2 A 3D Kinematic Previous: Two screws
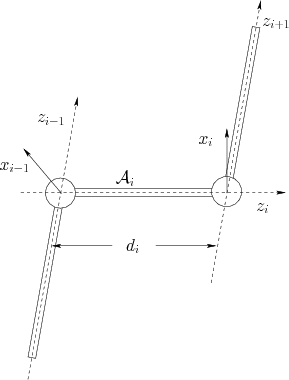
As in the 2D case, the first matrix, ![]() , is special. To represent
any position and orientation of
, is special. To represent
any position and orientation of
![]() , it could be defined as a
general rigid-body homogeneous transformation matrix,
(3.50). If the first body is only capable of rotation
via a revolute joint, then a simple convention is usually
followed. Let the
, it could be defined as a
general rigid-body homogeneous transformation matrix,
(3.50). If the first body is only capable of rotation
via a revolute joint, then a simple convention is usually
followed. Let the
![]() parameters of
parameters of ![]() be assigned as
be assigned as
![]() (there is no
(there is no ![]() -axis). This implies that
-axis). This implies that
![]() from (3.55) is the identity matrix, which makes
from (3.55) is the identity matrix, which makes ![]() .
.
The transformation ![]() for
for ![]() gives the relationship between
the body frame of
gives the relationship between
the body frame of
![]() and the body frame of
and the body frame of
![]() . The
position of a point
. The
position of a point ![]() on
on
![]() is given by
is given by
For each revolute joint, ![]() is treated as the only
variable in
is treated as the only
variable in ![]() . Prismatic joints can be
modeled by allowing
. Prismatic joints can be
modeled by allowing ![]() to vary. More complicated joints can be
modeled as a sequence of degenerate joints. For example, a
spherical joint can be considered as a sequence of three
zero-length revolute joints; the joints perform
a roll, a pitch, and a yaw. Another option for more complicated
joints is to abandon the DH representation and directly develop the
homogeneous transformation matrix. This might be needed to preserve
topological properties that become important in Chapter
4.
to vary. More complicated joints can be
modeled as a sequence of degenerate joints. For example, a
spherical joint can be considered as a sequence of three
zero-length revolute joints; the joints perform
a roll, a pitch, and a yaw. Another option for more complicated
joints is to abandon the DH representation and directly develop the
homogeneous transformation matrix. This might be needed to preserve
topological properties that become important in Chapter
4.
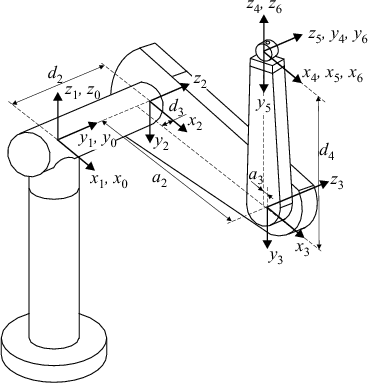 |
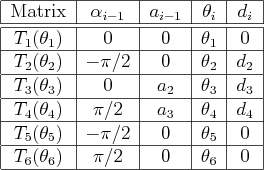 |
The parameters from Figure 3.17 may be substituted into the homogeneous transformation matrices to obtain
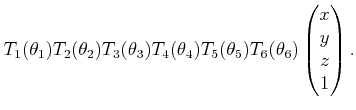 |
(3.64) |
 |
 |
 |
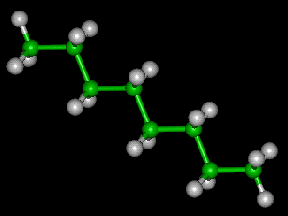
Note that the bonds correspond exactly to the axes of rotation. This
suggests that the ![]() axes should be chosen to coincide with the
bonds. Since consecutive bonds meet at atoms, there is no distance
between them. From Figure 3.15c, observe that this makes
axes should be chosen to coincide with the
bonds. Since consecutive bonds meet at atoms, there is no distance
between them. From Figure 3.15c, observe that this makes ![]() for all
for all ![]() . From Figure 3.15a, it can be seen that each
. From Figure 3.15a, it can be seen that each
![]() corresponds to a bond length, the distance between
consecutive carbon atoms. See Figure 3.20. This
leaves two angular parameters,
corresponds to a bond length, the distance between
consecutive carbon atoms. See Figure 3.20. This
leaves two angular parameters, ![]() and
and ![]() . Since the
only possible motion of the links is via rotation of the
. Since the
only possible motion of the links is via rotation of the ![]() -axes,
the angle between two consecutive axes, as shown in Figure
3.15d, must remain constant. In chemistry, this is referred
to as the bond angle and is represented in the DH
parameterization as
-axes,
the angle between two consecutive axes, as shown in Figure
3.15d, must remain constant. In chemistry, this is referred
to as the bond angle and is represented in the DH
parameterization as ![]() . The remaining
. The remaining ![]() parameters
are the variables that represent the degrees of freedom. However,
looking at Figure 3.15b, observe that the example is
degenerate because each
parameters
are the variables that represent the degrees of freedom. However,
looking at Figure 3.15b, observe that the example is
degenerate because each ![]() -axis has no frame of reference because
each
-axis has no frame of reference because
each ![]() . This does not, however, cause any problems. For
visualization purposes, it may be helpful to replace
. This does not, however, cause any problems. For
visualization purposes, it may be helpful to replace ![]() and
and
![]() by
by ![]() and
and ![]() , respectively. This way it is easy
to see that as the bond for the
, respectively. This way it is easy
to see that as the bond for the ![]() -axis is twisted, the observed
angle changes accordingly. Each bond is interpreted as a link,
-axis is twisted, the observed
angle changes accordingly. Each bond is interpreted as a link,
![]() . The origin of each
. The origin of each
![]() must be chosen to coincide with the
intersection point of the
must be chosen to coincide with the
intersection point of the ![]() - and
- and ![]() -axes. Thus, most of
the points in
-axes. Thus, most of
the points in
![]() will lie in the
will lie in the ![]() direction; see Figure
3.20.
direction; see Figure
3.20.
The next task is to write down the matrices. Attach a world frame to
the first bond, with the second atom at the origin and the bond
aligned with the ![]() -axis, in the negative direction; see Figure
3.20. To define
-axis, in the negative direction; see Figure
3.20. To define ![]() , recall that
, recall that ![]() from
(3.54) because
from
(3.54) because ![]() is dropped. The parameter
is dropped. The parameter ![]() represents the distance between the intersection points of the
represents the distance between the intersection points of the ![]() -
and
-
and ![]() -axes along the
-axes along the ![]() axis. Since there is no
axis. Since there is no ![]() -axis,
there is freedom to choose
-axis,
there is freedom to choose ![]() ; hence, let
; hence, let ![]() to obtain
to obtain
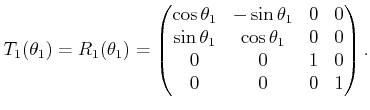 |
(3.65) |
The matrices for the remaining six bonds are
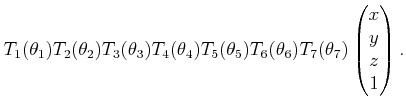 |
(3.67) |
Steven M LaValle 2020-08-14