Consider transforming a robot model. If 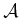 is expressed by naming
specific points in
is expressed by naming
specific points in
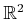 , as in a boundary representation of a
polygon, then each point is simply transformed from
, as in a boundary representation of a
polygon, then each point is simply transformed from 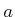 to
to
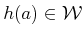 . In this case, it is straightforward to transform the entire
model using
. In this case, it is straightforward to transform the entire
model using 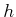 . However, there is a slight complication if the robot
model is expressed using primitives, such as
. However, there is a slight complication if the robot
model is expressed using primitives, such as
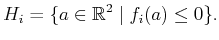 |
(3.22) |
This differs slightly from (3.2) because the robot is
defined in
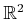 (which is not necessarily
(which is not necessarily 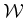 ), and also
), and also 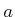 is
used to denote a point
is
used to denote a point
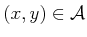 . Under a transformation
. Under a transformation 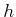 ,
the primitive is transformed as
,
the primitive is transformed as
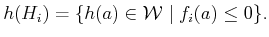 |
(3.23) |
To transform the primitive completely, however, it is better to
directly name points in
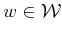 , as opposed to
, as opposed to
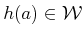 .
Using the fact that
.
Using the fact that
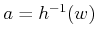 , this becomes
, this becomes
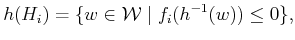 |
(3.24) |
in which the inverse of 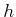 appears in the right side because the
original point
appears in the right side because the
original point 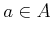 needs to be recovered to evaluate
needs to be recovered to evaluate 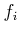 .
Therefore, it is important to be careful because either
.
Therefore, it is important to be careful because either 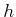 or
or 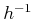 may be required to transform the model. This will be observed in more
specific contexts in some coming examples.
may be required to transform the model. This will be observed in more
specific contexts in some coming examples.
Steven M LaValle
2020-08-14

![]() is expressed by naming
specific points in
is expressed by naming
specific points in
![]() , as in a boundary representation of a
polygon, then each point is simply transformed from
, as in a boundary representation of a
polygon, then each point is simply transformed from ![]() to
to
![]() . In this case, it is straightforward to transform the entire
model using
. In this case, it is straightforward to transform the entire
model using ![]() . However, there is a slight complication if the robot
model is expressed using primitives, such as
. However, there is a slight complication if the robot
model is expressed using primitives, such as