
Next: Bitmaps Up: 3.1.3 Other Models Previous: 3D triangles
These are used in many engineering design systems to allow convenient design and adjustment of curved surfaces, in applications such as aircraft or automobile body design. In contrast to semi-algebraic models, which are implicit equations, NURBS and other splines are parametric equations. This makes computations such as rendering easier; however, others, such as collision detection, become more difficult. These models may be defined in any dimension. A brief 2D formulation is given here.
A curve can be expressed as
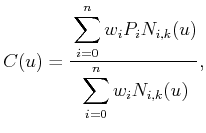 |
(3.18) |
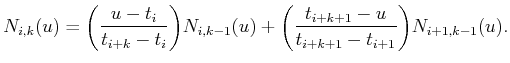 |
(3.19) |
Steven M LaValle 2020-08-14