
Next: 15.5.3 Other Steering Methods Up: 15.5.2 Using Sinusoidal Action Previous: 15.5.2.2 First-order controllable systems
Example 15.17 considered a special case of a
chained-form system. The system in (15.102) can be
generalized to any ![]() as
as
| (15.161) |
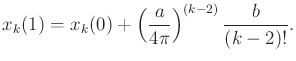 |
(15.162) |
For a proof of the correctness of the second phase, and more information in general, see [727,846]. It may appear that very few systems fit the forms given in this section; however, it is sometimes possible to transform systems to fit this form. Recall that the original simple car model in (13.15) was simplified to (15.54). Transformation methods for putting systems into chained form have been developed. For systems that still cannot be put in this form, Fourier techniques can be used to obtain approximate steering methods that are similar in spirit to the methods in this section. When the chained-form system is expressed using Pfaffian constraints, the result is often referred to as the Goursat normal form. The method can be extended even further to multi-chained-form systems.
Steven M LaValle 2020-08-14