
Next: 15.5 Steering Methods for Up: 15.4.3 Determining Controllability Previous: 15.4.3.4 Controllability of driftless
Determining whether a system with drift (15.52), is STLC
is substantially more difficult. Imagine a mechanical system, such as
a hovercraft, that is moving at a high speed. Due to momentum, it is
impossible from most states to move in certain directions during an
arbitrarily small interval of time. One can, however, ask whether a
system is STLC from a state ![]() for which
for which
![]() . For a
mechanical system, this usually means that it starts at rest. If a
system with drift is STLC, this intuitively means that it can move in
any direction by hovering around states that are close to zero
velocity for the mechanical system.
. For a
mechanical system, this usually means that it starts at rest. If a
system with drift is STLC, this intuitively means that it can move in
any direction by hovering around states that are close to zero
velocity for the mechanical system.
The Lie algebra techniques can be extended to determine
controllability for systems with drift; however, the tools needed are
far more complicated. See Chapter 7 of [156] for more
complete coverage. Even if
![]() , it does not
necessarily imply that the system is STLC. It does at least imply
that the system is accessible, which motivates the definition given in
Section 15.1.3. Thus, the set of achievable
velocities still has dimension
, it does not
necessarily imply that the system is STLC. It does at least imply
that the system is accessible, which motivates the definition given in
Section 15.1.3. Thus, the set of achievable
velocities still has dimension ![]() ; however, motions in all directions
may not be possible due to drift. To obtain STLC, a sufficient
condition is that the set of possible values for
; however, motions in all directions
may not be possible due to drift. To obtain STLC, a sufficient
condition is that the set of possible values for ![]() contains an
open set that contains the origin.
contains an
open set that contains the origin.
The following example clearly illustrates the main difficultly with establishing whether a system with drift is STLC.
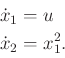 |
(15.111) |
| (15.112) |
| (15.113) |
In Example 15.20,
![]() was an example of a
bad bracket [925] because it obstructed controllability.
A method of classifying brackets as good or bad has been
developed, and there exist theorems that imply whether a system with
drift is STLC by satisfying certain conditions on the good and bad
brackets. Intuitively, there must be enough good brackets to
neutralize the obstructions imposed by the bad brackets
[156,925].
was an example of a
bad bracket [925] because it obstructed controllability.
A method of classifying brackets as good or bad has been
developed, and there exist theorems that imply whether a system with
drift is STLC by satisfying certain conditions on the good and bad
brackets. Intuitively, there must be enough good brackets to
neutralize the obstructions imposed by the bad brackets
[156,925].
Steven M LaValle 2020-08-14