The notion of a Lie algebra is first established in general. Let 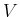 be any vector space with coefficients in
be any vector space with coefficients in
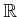 . In
. In 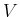 , the vectors
can be added or multiplied by elements of
, the vectors
can be added or multiplied by elements of
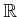 ; however, there is no
way to ``multiply'' two vectors to obtain a third. The Lie algebra
introduces a product operation to
; however, there is no
way to ``multiply'' two vectors to obtain a third. The Lie algebra
introduces a product operation to 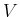 . The product is called a
bracket or Lie bracket (considered here as a
generalization of the previous Lie bracket) and is denoted by
. The product is called a
bracket or Lie bracket (considered here as a
generalization of the previous Lie bracket) and is denoted by
![$ [\cdot,\cdot]: V \times V \rightarrow V$](img6848.gif) .
.
Example 15..14 (The Vector Cross Product)
Let
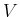
be the vector space over
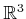
that is used in vector
calculus. The basis elements are often denoted as
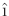
,
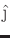
, and
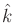
. A bracket for this vector space is simply
the cross product
![$\displaystyle [u,v] = u \times v .$](img6858.gif) |
(15.98) |
It can be verified that the required axioms of a Lie bracket are
satisfied.
One interesting property of the cross product that is exploited often
in analytic geometry is that it produces a vector outside of the span
of 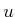 and
and 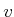 . For example, let
. For example, let 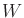 be the two-dimensional subspace
of vectors
be the two-dimensional subspace
of vectors
 |
(15.99) |
The cross product always yields a vector that is a multiple of
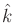
, which lies outside of
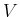
if the product is nonzero. This
behavior is very similar to constructing vector fields that lie
outside of
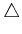
using the Lie bracket in Section
15.4.2.

Example 15..15 (Lie Algebra on Lie Groups)
Lie groups are the most important
application of the Lie algebra concepts. Recall from Section
4.2.1 the notion of a matrix group. Important
examples throughout this book have been
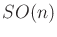
and
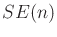
. If
interpreted as a smooth manifold, these matrix groups are examples of
Lie groups [
63]
. In general, a
Lie
group 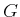
is both a differentiable manifold and a group with
respect to some operation
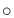
if and only if:
- The product
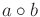 , interpreted as a function from
, interpreted as a function from
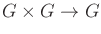 , is smooth.
, is smooth.
- The inverse
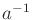 , interpreted as a function from
, interpreted as a function from 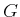 to
to 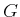 , is smooth.
, is smooth.
The two conditions are needed to prevent the group from destroying the
nice properties that come with the smooth manifold. An important
result in the study of Lie groups is that all compact
finite-dimensional Lie groups can be represented as matrix groups.
For any Lie group, a Lie algebra can be defined on a special set of
vector fields. These are defined using the left translation
mapping
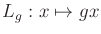 . The vector field formed from the
differential of
. The vector field formed from the
differential of 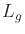 is called a left-invariant vector field.
A Lie algebra can be defined on the set of these fields.
The Lie bracket definition depends on the particular group. For the
case of
is called a left-invariant vector field.
A Lie algebra can be defined on the set of these fields.
The Lie bracket definition depends on the particular group. For the
case of 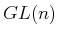 , the Lie bracket is
, the Lie bracket is
![$\displaystyle [A,B] = AB - BA .$](img6864.gif) |
(15.100) |
In this case, the Lie bracket clearly appears to be a test for
commutativity. If the matrices commute with respect to
multiplication, then the Lie bracket is zero. The Lie brackets for
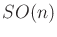
and
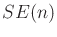
are given in many texts on mechanics and control
[
156,
846]. The Lie algebra of left-invariant vector
fields is an important structure in the study of nonlinear systems and
mechanics.


![]() be any vector space with coefficients in
be any vector space with coefficients in
![]() . In
. In ![]() , the vectors
can be added or multiplied by elements of
, the vectors
can be added or multiplied by elements of
![]() ; however, there is no
way to ``multiply'' two vectors to obtain a third. The Lie algebra
introduces a product operation to
; however, there is no
way to ``multiply'' two vectors to obtain a third. The Lie algebra
introduces a product operation to ![]() . The product is called a
bracket or Lie bracket (considered here as a
generalization of the previous Lie bracket) and is denoted by
. The product is called a
bracket or Lie bracket (considered here as a
generalization of the previous Lie bracket) and is denoted by
![]() .
.
![]() , the bracket must satisfy
the following three axioms:
, the bracket must satisfy
the following three axioms:
![\begin{displaymath}\begin{split}[a u + b v, w]& = a [u,w] + b [v,w] \\ [u, a v + b w] & = a [u,w] + b [u,w] . \\ \end{split}\end{displaymath}](img6850.gif)
![]() and
and ![]() . For example, let
. For example, let ![]() be the two-dimensional subspace
of vectors
be the two-dimensional subspace
of vectors
![]() . The vector field formed from the
differential of
. The vector field formed from the
differential of ![]() is called a left-invariant vector field.
A Lie algebra can be defined on the set of these fields.
The Lie bracket definition depends on the particular group. For the
case of
is called a left-invariant vector field.
A Lie algebra can be defined on the set of these fields.
The Lie bracket definition depends on the particular group. For the
case of ![]() , the Lie bracket is
, the Lie bracket is