Interesting interpretations of the minimum principle exist for the
case of optimizing the time to reach the goal [424,903].
In this case,
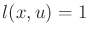 in (15.26), and the cost term
can be ignored. For the remaining portion, let
in (15.26), and the cost term
can be ignored. For the remaining portion, let 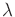 be defined
as
be defined
as
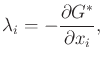 |
(15.40) |
instead of using (15.25). In this case, the Hamiltonian
can be expressed as
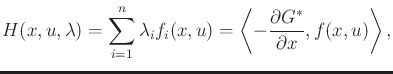 |
(15.41) |
which is an inner product between 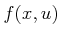 and the negative gradient
of
and the negative gradient
of 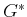 . Using (15.40), the Hamiltonian should be
maximized instead of minimized (this is equivalent to Pontryagin's
original formulation [801]). An inner product of two
vectors increases as their directions become closer to parallel.
Optimizing (15.41) amounts to selecting
. Using (15.40), the Hamiltonian should be
maximized instead of minimized (this is equivalent to Pontryagin's
original formulation [801]). An inner product of two
vectors increases as their directions become closer to parallel.
Optimizing (15.41) amounts to selecting 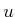 so that
so that
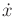 is as close as possible to the direction of steepest descent
of
is as close as possible to the direction of steepest descent
of 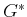 . This is nicely interpreted by considering how the
boundary of the reachable set
. This is nicely interpreted by considering how the
boundary of the reachable set
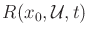 propagates through
propagates through  .
By definition, the points on
.
By definition, the points on
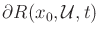 must correspond to
time-optimal trajectories. Furthermore,
must correspond to
time-optimal trajectories. Furthermore,
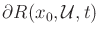 can be
interpreted as a propagating wavefront that is perpendicular to
can be
interpreted as a propagating wavefront that is perpendicular to
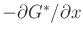 . The minimum principle simply indicates
that
. The minimum principle simply indicates
that 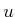 should be chosen so that
should be chosen so that 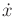 points into the propagating
boundary, as close to being orthogonal as possible [424].
points into the propagating
boundary, as close to being orthogonal as possible [424].
Steven M LaValle
2020-08-14

![]() in (15.26), and the cost term
can be ignored. For the remaining portion, let
in (15.26), and the cost term
can be ignored. For the remaining portion, let ![]() be defined
as
be defined
as